Valid Square
Problem Description
Given the coordinates of four points in 2D space p1, p2, p3 and p4, return true if the four points construct a square.
The coordinate of a point pi is represented as [xi, yi]. The input is not given in any order.
A valid square has four equal sides with positive length and four equal angles (90-degree angles).
Examples
Example 1:
Input: p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,1]
Output: true
Example 2:
Input: p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,12]
Output: false
Constraints
p1.length == p2.length == p3.length == p4.length == 2
Solution for Valid Square
Approach: Using Sorting
We can make use of maths to simplify this problem a bit. If we sort the given set of points based on their x-coordinate values, and in the case of a tie, based on their y-coordinate value, we can obtain an arrangement, which directly reflects the arrangement of points on a valid square boundary possible.
Consider the only possible cases as shown in the figure below:
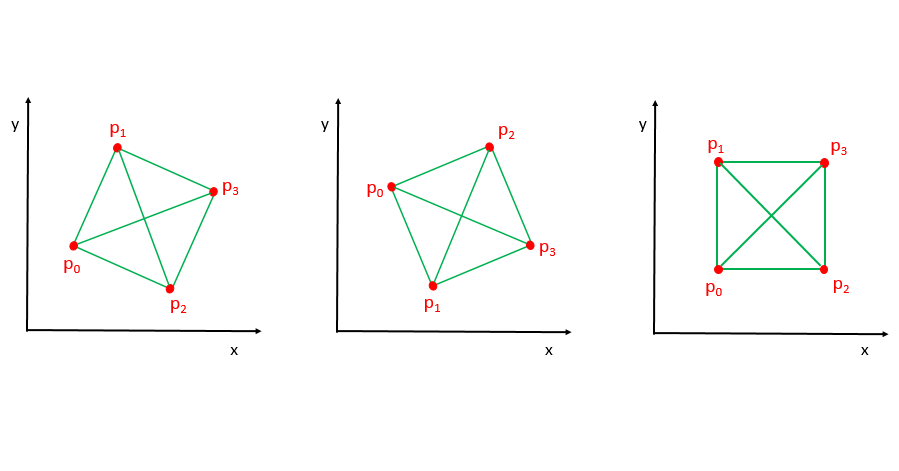
-
p0p1, p1p3, p3p2 and p2p0 form the four sides of any valid square.
-
p0p3 and p1p2 form the diagonals of the square.
Thus, once the sorting of the points is done, based on the above knowledge, we can directly compare p0p1, p1p3, p3p2 and p2p0 or equality of lengths(corresponding to the sides); and p0p3 and p1p2 for equality of lengths(corresponding to the diagonals).
Code in Different Languages
- C++
- Java
- Python
#include <cmath>
#include <algorithm>
#include <vector>
class Solution {
public:
double dist(std::vector<int>& p1, std::vector<int>& p2) {
return (p2[1] - p1[1]) * (p2[1] - p1[1]) + (p2[0] - p1[0]) * (p2[0] - p1[0]);
}
bool validSquare(std::vector<int>& p1, std::vector<int>& p2, std::vector<int>& p3, std::vector<int>& p4) {
std::vector<std::vector<int>> p = {p1, p2, p3, p4};
std::sort(p.begin(), p.end(), [](const std::vector<int>& l1, const std::vector<int>& l2) {
return l1[0] != l2[0] ? l1[0] < l2[0] : l1[1] < l2[1];
});
return dist(p[0], p[1]) != 0 && dist(p[0], p[1]) == dist(p[1], p[3]) && dist(p[1], p[3]) == dist(p[3], p[2]) && dist(p[3], p[2]) == dist(p[2], p[0]) && dist(p[0], p[3]) == dist(p[1], p[2]);
}
};
public class Solution {
public double dist(int[] p1, int[] p2) {
return (p2[1] - p1[1]) * (p2[1] - p1[1]) + (p2[0] - p1[0]) * (p2[0] - p1[0]);
}
public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) {
int[][] p={p1,p2,p3,p4};
Arrays.sort(p, (l1, l2) -> l2[0] == l1[0] ? l1[1] - l2[1] : l1[0] - l2[0]);
return dist(p[0], p[1]) != 0 && dist(p[0], p[1]) == dist(p[1], p[3]) && dist(p[1], p[3]) == dist(p[3], p[2]) && dist(p[3], p[2]) == dist(p[2], p[0]) && dist(p[0],p[3])==dist(p[1],p[2]);
}
}
import math
class Solution:
def dist(self, p1, p2):
return (p2[1] - p1[1]) ** 2 + (p2[0] - p1[0]) ** 2
def validSquare(self, p1, p2, p3, p4):
points = [p1, p2, p3, p4]
points.sort(key=lambda x: (x[0], x[1]))
return self.dist(points[0], points[1]) != 0 and \
self.dist(points[0], points[1]) == self.dist(points[1], points[3]) and \
self.dist(points[1], points[3]) == self.dist(points[3], points[2]) and \
self.dist(points[3], points[2]) == self.dist(points[2], points[0]) and \
self.dist(points[0], points[3]) == self.dist(points[1], points[2])
Complexity Analysis
Time Complexity:
Reason: Sorting 4 points takes constant time.
Space Complexity:
Reason: Constant space is required.
References
-
LeetCode Problem: Valid Square
-
Solution Link: Valid Square