01 Matrix

Problem Description

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Examples

Example 1:

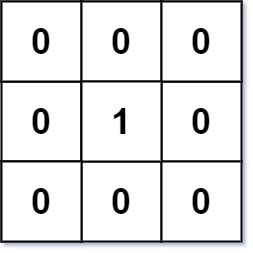
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

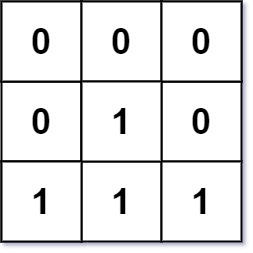
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 10^4
• 1 <= m * n <= 10^4
• mat[i][j] is either 0 or 1.
• There is at least one 0 in mat.

Solution for 542. 01 Matrix Problem

Approach

1. Initialization:

   • Create a queue q to perform a Breadth-First Search (BFS).
   • Create a vis matrix to keep track of visited cells.
   • Create a dis matrix to store the distance of each cell from the nearest 0.

2. Enqueue All Zeros:

   • Iterate through each cell in the matrix.
   • If a cell contains 0, enqueue it with a distance of 0 and mark it as visited in the vis matrix.
   • If a cell contains 1, mark it as not visited in the vis matrix.

3. Define Directions:

   • Define arrays drow and dcol to represent the four possible directions (up, right, down, left).

4. BFS Traversal:

   • While the queue is not empty:
     • Dequeue the front element.
     • For each direction:
       • Calculate the new row and column indices.
       • Check if the new indices are within the bounds and the cell is not visited.
       • If valid, mark the cell as visited, enqueue it with the incremented distance, and update the dis matrix.

5. Return Result:

   • After the BFS completes, the dis matrix contains the required distances.

Solution

Implementation

Live Editor

function Solution(arr) {
var updateMatrix = function(mat) {
    let n = mat.length;
    let m = mat[0].length;

    let q = [];
    let vis = Array.from({ length: n }, () => Array(m).fill(0));
    let dis = Array.from({ length: n }, () => Array(m).fill(0));

    for (let i = 0; i < n; i++) {
        for (let j = 0; j < m; j++) {
            if (mat[i][j] === 0) {
                q.push([[i, j], 0]);
                vis[i][j] = 1;
            } else {
                vis[i][j] = 0;
            }
        }
    }
    let drow = [-1, 0, 1, 0];
    let dcol = [0, 1, 0, -1];

    while (q.length) {
        let [pos, steps] = q.shift();
        let [row, col] = pos;
        dis[row][col] = steps;
        for (let i = 0; i < 4; i++) {
            let nrow = row + drow[i];
            let ncol = col + dcol[i];
            if (nrow >= 0 && ncol >= 0 && nrow < n && ncol < m && vis[nrow][ncol] === 0) {
                vis[nrow][ncol] = 1;
                q.push([[nrow, ncol], steps + 1]);
            }
        }
    }
    return dis;
};

  const input = [[0,0,0],[0,1,0],[1,1,1]]
  const output = updateMatrix(input)
  return (
    <div>
      <p>
        <b>Input: </b>
        {JSON.stringify(input)}
      </p>
      <p>
        <b>Output:</b> {output.toString()}
      </p>
    </div>
  );
}

Result

Loading...

Complexity Analysis

• Time Complexity: $O(n*m)$
• Space Complexity: $O(n*m)$

Code in Different Languages

JavaScript

Written by @hiteshgahanolia

var updateMatrix = function(mat) {
 let n = mat.length;
 let m = mat[0].length;

 let q = [];
 let vis = Array.from({ length: n }, () => Array(m).fill(0));
 let dis = Array.from({ length: n }, () => Array(m).fill(0));

 for (let i = 0; i < n; i++) {
     for (let j = 0; j < m; j++) {
         if (mat[i][j] === 0) {
             q.push([[i, j], 0]);
             vis[i][j] = 1;
         } else {
             vis[i][j] = 0;
         }
     }
 }
 let drow = [-1, 0, 1, 0];
 let dcol = [0, 1, 0, -1];

 while (q.length) {
     let [pos, steps] = q.shift();
     let [row, col] = pos;
     dis[row][col] = steps;
     for (let i = 0; i < 4; i++) {
         let nrow = row + drow[i];
         let ncol = col + dcol[i];
         if (nrow >= 0 && ncol >= 0 && nrow < n && ncol < m && vis[nrow][ncol] === 0) {
             vis[nrow][ncol] = 1;
             q.push([[nrow, ncol], steps + 1]);
         }
     }
 }
 return dis;
};

Python

Written by @hiteshgahanolia

from collections import deque

class Solution:
 def updateMatrix(self, mat):
     n = len(mat)
     m = len(mat[0])

     q = deque()
     vis = [[0 for _ in range(m)] for _ in range(n)]
     dis = [[0 for _ in range(m)] for _ in range(n)]

     for i in range(n):
         for j in range(m):
             if mat[i][j] == 0:
                 q.append(((i, j), 0))
                 vis[i][j] = 1
             else:
                 vis[i][j] = 0

     drow = [-1, 0, 1, 0]
     dcol = [0, 1, 0, -1]

     while q:
         (row, col), steps = q.popleft()
         dis[row][col] = steps
         for i in range(4):
             nrow = row + drow[i]
             ncol = col + dcol[i]
             if 0 <= nrow < n and 0 <= ncol < m and vis[nrow][ncol] == 0:
                 vis[nrow][ncol] = 1
                 q.append(((nrow, ncol), steps + 1))

     return dis

Java

Written by @hiteshgahanolia

import java.util.LinkedList;
import java.util.Queue;

public class Solution {
 public int[][] updateMatrix(int[][] mat) {
     int n = mat.length;
     int m = mat[0].length;

     Queue<int[]> q = new LinkedList<>();
     int[][] vis = new int[n][m];
     int[][] dis = new int[n][m];

     for (int i = 0; i < n; i++) {
         for (int j = 0; j < m; j++) {
             if (mat[i][j] == 0) {
                 q.add(new int[]{i, j, 0});
                 vis[i][j] = 1;
             } else {
                 vis[i][j] = 0;
             }
         }
     }
     int[] drow = {-1, 0, 1, 0};
     int[] dcol = {0, 1, 0, -1};

     while (!q.isEmpty()) {
         int[] current = q.poll();
         int row = current[0];
         int col = current[1];
         int steps = current[2];
         dis[row][col] = steps;
         for (int i = 0; i < 4; i++) {
             int nrow = row + drow[i];
             int ncol = col + dcol[i];
             if (nrow >= 0 && ncol >= 0 && nrow < n && ncol < m && vis[nrow][ncol] == 0) {
                 vis[nrow][ncol] = 1;
                 q.add(new int[]{nrow, ncol, steps + 1});
             }
         }
     }
     return dis;
 }
}

C++

Written by @hiteshgahanolia

class Solution {
public:
 vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
     int n = mat.size();
     int m = mat[0].size();

     queue<pair<pair<int, int>, int>> q;
     vector<vector<int>> vis(n, vector<int>(m, 0));
     vector<vector<int>> dis(n, vector<int>(m, 0));

     for (int i = 0; i < n; i++) {
         for (int j = 0; j < m; j++) {
             if (mat[i][j] == 0) {
                 q.push({{i, j}, 0});
                 vis[i][j] = 1;
             } else {
                 vis[i][j] = 0;
             }
         }
     }
     int drow[] = {-1, 0, 1, 0};
     int dcol[] = {0, 1, 0, -1};

     while (!q.empty()) {
         int row = q.front().first.first;
         int col = q.front().first.second;
         int steps = q.front().second;
         q.pop();
         dis[row][col] = steps;
         for (int i = 0; i < 4; i++) {
             int nrow = row + drow[i];
             int ncol = col + dcol[i];
             if (nrow >= 0 && ncol >= 0 && nrow < n && ncol < m && vis[nrow][ncol] == 0) {
                 vis[nrow][ncol] = 1;
                 q.push({{nrow, ncol}, steps + 1});
             }
         }
     }
     return dis;
 }
};

References

• LeetCode Problem: 542. 01 Matrix

• Solution Link: LeetCode Solution