Array Nesting

Problem Description

You are given an integer array nums of length n where nums is a permutation of the numbers in the range [0, n - 1].

You should build a set s[k] = {nums[k], nums[nums[k]], nums[nums[nums[k]]], ... } subjected to the following rule:

• The first element in s[k] starts with the selection of the element nums[k] of index = k.
• The next element in s[k] should be nums[nums[k]], and then nums[nums[nums[k]]], and so on.
• We stop adding right before a duplicate element occurs in s[k].
• Return the longest length of a set s[k].

Examples

Example 1:

Input: nums = [5,4,0,3,1,6,2]
Output: 4
Explanation: 
nums[0] = 5, nums[1] = 4, nums[2] = 0, nums[3] = 3, nums[4] = 1, nums[5] = 6, nums[6] = 2.
One of the longest sets s[k]:
s[0] = {nums[0], nums[5], nums[6], nums[2]} = {5, 6, 2, 0}

Example 2:

Input: nums = [0,1,2]
Output: 1

Constraints

• $1 <= nums.length <= 10^5$
• $0 <= nums[i] < nums.length$
• All the values of nums are unique.

Solution for Array Nesting

Approach #1 Brute Force [Time Limit Exceeded]

The simplest method is to iterate over all the indices of the given nums array. For every index i chosen, we find the element nums[i] and increment the count for a new element added for the current index i. Since nums[i] has to act as the new index for finding the next element belonging to the set corresponding to the index i, the new index is j=nums[i].

We continue this process of index updation and keep on incrementing the count for new elements added to the set corresponding to the index i. Now, since all the elements in nums lie in the range (0,...,N−1), the new indices generated will never lie outside the array size limits. But, we'll always reach a point where the current element becomes equal to the element nums[i] with which we started the nestings in the first place. Thus, after this, the new indices generated will be just the repetitions of the previously generated ones, and thus would not lead to an increase in the size of the current set. Thus, this condition of the current number being equal to the starting number acts as the terminating condition for count incrementation for a particular index.

We do the same process for every index chosen as the starting index. At the end, the maximum value of count obtained gives the size of the largest set.

Code in Different Languages

C++

Written by @Shreyash3087

#include <vector>
#include <algorithm>  // For std::max

class Solution {
public:
    int arrayNesting(std::vector<int>& nums) {
        int res = 0;
        int n = nums.size();
        std::vector<bool> visited(n, false);
        
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                int start = nums[i], count = 0;
                do {
                    start = nums[start];
                    count++;
                    visited[start] = true;
                } while (start != nums[i]);
                res = std::max(res, count);
            }
        }
        return res;
    }
};

Java

Written by @Shreyash3087

public class Solution {
    public int arrayNesting(int[] nums) {
        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            int start = nums[i], count = 0;
            do {
                start = nums[start];
                count++;
            }
            while (start != nums[i]);
            res = Math.max(res, count);

        }
        return res;
    }
}

Python

Written by @Shreyash3087

class Solution:
    def arrayNesting(self, nums):
        res = 0
        visited = [False] * len(nums)
        
        for i in range(len(nums)):
            if not visited[i]:
                start = nums[i]
                count = 0
                while True:
                    start = nums[start]
                    count += 1
                    visited[start] = True
                    if start == nums[i]:
                        break
                res = max(res, count)
                
        return res

Complexity Analysis

Time Complexity: $O(N^2)$

Reason: In worst case, for example- [1,2,3,4,5,0], loop body will be executed $N^2$ times.

Space Complexity: $O(1)$

Reason: Constant space is used.

Approach #2 Using Visited Array

Algorithm

In the last approach, we observed that in the worst case, all the elements of the nums array are added to the sets corresponding to all the starting indices. But, all these sets correspond to the same set of elements only, leading to redundant calculations.

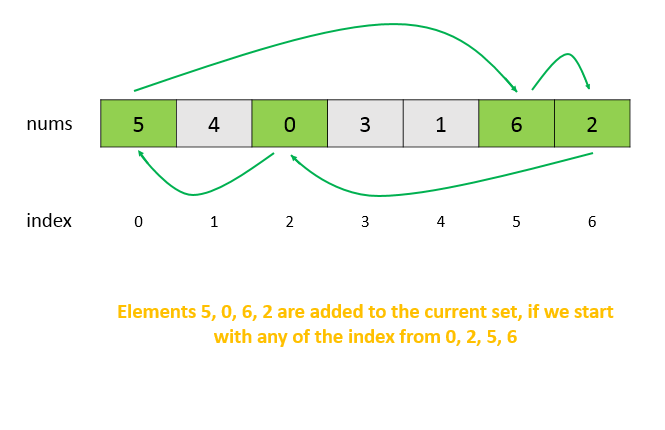
We consider a simple example and see how this problem can be resolved. From the figure below, we can see that the elements in the current nesting shown by arrows form a cycle. Thus, the same elements will be added to the current set irrespective of the first element chosen to be added to the set out of these marked elements.

Thus, when we add an element nums[j] to a set corresponding to any of the indices, we mark its position as visited in a visited array. This is done so that whenever this index is chosen as the starting index in the future, we do not go for redundant count calculations, since we've already considered the elements linked with this index, which will be added to a new(duplicate) set.

By doing so, we ensure that the duplicate sets aren't considered again and again.

Further, we can also observe that no two elements at indices i and j will lead to a jump to the same index k, since it would require nums[i]=nums[j]=k, which isn't possible since all the elements are distinct. Also, because of the same reasoning, no element outside any cycle could lead to an element inside the cycle. Because of this, the use of visited array goes correctly.

Code in Different Languages

C++

Written by @Shreyash3087

#include <vector>
#include <algorithm>  // For std::max

class Solution {
public:
    int arrayNesting(std::vector<int>& nums) {
        std::vector<bool> visited(nums.size(), false);
        int res = 0;
        
        for (int i = 0; i < nums.size(); i++) {
            if (!visited[i]) {
                int start = nums[i], count = 0;
                do {
                    start = nums[start];
                    count++;
                    visited[start] = true;
                } while (start != nums[i]);
                res = std::max(res, count);
            }
        }
        return res;
    }
};

Java

Written by @Shreyash3087

public class Solution {
    public int arrayNesting(int[] nums) {
        boolean[] visited = new boolean[nums.length];
        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            if (!visited[i]) {
                int start = nums[i], count = 0;
                do {
                    start = nums[start];
                    count++;
                    visited[start] = true;
                }
                while (start != nums[i]);
                res = Math.max(res, count);
            }
        }
        return res;
    }
}

Python

Written by @Shreyash3087

class Solution:
    def arrayNesting(self, nums):
        visited = [False] * len(nums)
        res = 0
        
        for i in range(len(nums)):
            if not visited[i]:
                start = nums[i]
                count = 0
                while True:
                    start = nums[start]
                    count += 1
                    visited[start] = True
                    if start == nums[i]:
                        break
                res = max(res, count)
                
        return res

Complexity Analysis

Time Complexity: $O(N)$

Reason: Every element of the nums array will be considered at most once.

Space Complexity: $O(N)$

Reason: visited array of size N is used.

References

• LeetCode Problem: Array Nesting

• Solution Link: Array Nesting

---

Authors:

Loading...