Number of Provinces
Problem Description
There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c. A province is a group of directly or indirectly connected cities and no other cities outside of the group. You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise. Return the total number of provinces.
Examples
Example 1:
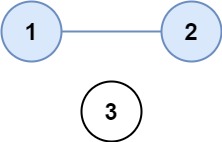
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2
Example 2:
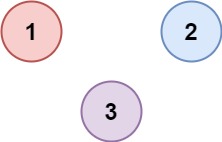
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
Constraints
1 <= n <= 200n == isConnected.lengthn == isConnected[i].lengthisConnected[i][j] is 1 or 0.isConnected[i][i] == 1isConnected[i][j] == isConnected[j][i]
Solution for Number of Provinces
Intuition ans Approach
-
To find the solution, we conceptualize the cities and the connections between them as a graph, where each city is a node and each direct connection is an edge. Now, the problem translates to finding the number of connected components in the graph. Each connected component will represent one province.
-
To do this, we use Depth-First Search (DFS). Here's the intuition behind using DFS:
-
We start with the first city and perform a DFS to mark all cities that are connected directly or indirectly to it. These cities form one province.
-
Once the DFS is completed, we look for the next city that hasn't been visited yet and perform a DFS from that city to find another province.
-
We repeat this process until all cities have been visited.
-
Each time we initiate a DFS from a new unvisited city, we know that we've found a new province, so we increment our province count. The DFS ensures that we navigate through all the cities within a province before moving on to the next one.
-
By doing the above steps using a vis (visited) list to keep track of which cities have been visited, we can effectively determine and count all the provinces.
- Solution
Implementation
function Solution() { function dfs(root, vis, adj) { vis[root] = 1; for (let val of adj[root]) { if (vis[val] === 0) { dfs(val, vis, adj); } } } function findCircleNum(isConnected) { const n = isConnected.length; let cnt = 0; const vis = new Array(n + 1).fill(0); const adj = Array.from({ length: n + 1 }, () => []); // Build adjacency list for (let i = 0; i < n; i++) { for (let j = 0; j < n; j++) { if (i !== j && isConnected[i][j] === 1) { adj[i + 1].push(j + 1); } } } // Find all provinces for (let i = 1; i <= n; i++) { if (vis[i] === 0) { cnt++; dfs(i, vis, adj); } } return cnt; } const input = [[1,1,0],[1,1,0],[0,0,1]] const output = findCircleNum(input); return ( <div> <p> <b>Input: </b>{JSON.stringify(input)} </p> <p> <b>Output:</b> {output.toString()} </p> </div> ); }
Code in Different Languages
- JavaScript
- TypeScript
- Python
- Java
- C++
function dfs(root, vis, adj) {
vis[root] = 1;
for (let val of adj[root]) {
if (vis[val] === 0) {
dfs(val, vis, adj);
}
}
}
function findCircleNum(isConnected) {
const n = isConnected.length;
let cnt = 0;
const vis = new Array(n + 1).fill(0);
const adj = Array.from({ length: n + 1 }, () => []);
// Build adjacency list
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
if (i !== j && isConnected[i][j] === 1) {
adj[i + 1].push(j + 1);
}
}
}
// Find all provinces
for (let i = 1; i <= n; i++) {
if (vis[i] === 0) {
cnt++;
dfs(i, vis, adj);
}
}
return cnt;
}
class Solution {
dfs(root: number, vis: number[], adj: number[][]): void {
vis[root] = 1;
for (let val of adj[root]) {
if (vis[val] === 0) {
this.dfs(val, vis, adj);
}
}
}
findCircleNum(isConnected: number[][]): number {
const n = isConnected.length;
let cnt = 0;
const vis = new Array(n + 1).fill(0);
const adj: number[][] = Array.from({ length: n + 1 }, () => []);
// Build adjacency list
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
if (i !== j && isConnected[i][j] === 1) {
adj[i + 1].push(j + 1);
}
}
}
// Find all provinces
for (let i = 1; i <= n; i++) {
if (vis[i] === 0) {
cnt++;
this.dfs(i, vis, adj);
}
}
return cnt;
}
}
class Solution:
def dfs(self, root, vis, adj):
vis[root] = 1
for val in adj[root]:
if not vis[val]:
self.dfs(val, vis, adj)
def findCircleNum(self, isConnected):
n = len(isConnected)
cnt = 0
vis = [0] * (n + 1)
adj = [[] for _ in range(n + 1)]
# Build adjacency list
for i in range(n):
for j in range(n):
if i != j and isConnected[i][j] == 1:
adj[i + 1].append(j + 1)
# Find all provinces
for i in range(1, n + 1):
if not vis[i]:
cnt += 1
self.dfs(i, vis, adj)
return cnt
import java.util.*;
class Solution {
public void dfs(int root, int[] vis, List<Integer>[] adj) {
vis[root] = 1;
for (int val : adj[root]) {
if (vis[val] == 0) {
dfs(val, vis, adj);
}
}
}
public int findCircleNum(int[][] isConnected) {
int n = isConnected.length;
int cnt = 0;
int[] vis = new int[n + 1];
List<Integer>[] adj = new ArrayList[n + 1];
for (int i = 0; i <= n; i++) {
adj[i] = new ArrayList<>();
}
// Build adjacency list
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j && isConnected[i][j] == 1) {
adj[i + 1].add(j + 1);
}
}
}
// Find all provinces
for (int i = 1; i <= n; i++) {
if (vis[i] == 0) {
cnt++;
dfs(i, vis, adj);
}
}
return cnt;
}
}
class Solution {
public:
void dfs(int root, vector<int>& vis, vector<int> adj[]){
vis[root]=1;
for (auto val : adj[root]){
if(!vis[val]){
dfs(val,vis,adj);
}
}
}
int findCircleNum(vector<vector<int>>& isConnected) {
int n= isConnected.size();
int cnt=0;
vector<int> vis(n+1,0);
vector<int> adj[n+1];
for (int i=0; i<n; i++){
for (int j=0; j<n; j++){
if (i!=j && isConnected[i][j]){
adj[i+1].push_back(j+1);
}
}
}
for (int i=1; i<=n; i++){
if(!vis[i]){
cnt++;
dfs(i,vis,adj);
}
}
return cnt;
}
};
Complexity Analysis
Time Complexity:
-
The time complexity of the algorithm is , where N is the number of vertices (or cities) in the graph. This complexity arises because the algorithm involves visiting every vertex once and, for each vertex, iterating through all possible adjacent vertices to explore the edges. In the worst-case scenario, this results in checking every entry in the isConnected matrix once, which has entries.
-
The dfs function explores all connected vertices through recursive calls. Since each edge and vertex will only be visited once in the DFS traversal, the total number of operations performed will be related to the total number of vertices and edges. However, because the graph is represented by an N x N adjacency matrix and it must be fully inspected to discover all connections, the time is bounded by the size of the matrix .
Space Complexity:
The space complexity of the algorithm is , which comes from the following:
- The recursion stack for DFS, which in the worst case, could store up to N frames if the graph is implemented as a linked structure such as a list of nodes (a path with all nodes connected end-to-end).
- The vis visited array, which is a boolean array of length N used to track whether each vertex has been visited or not to prevent cycles during the DFS.
- Given that N recursion calls could happen in a singly connected component spanning all the vertices, the space taken by the call stack should be considered in the final space complexity, merging it with the space taken by the array to .
References
-
LeetCode Problem: Number of Provinces
-
Solution Link: LeetCode Solution