Binary Tree Tilt
Problem Description
Given the root of a binary tree, return the sum of every tree node's tilt.
The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.
Examples
Example 1:
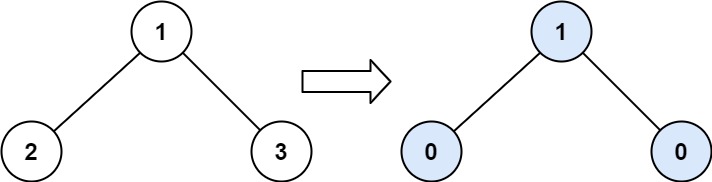
Input: root = [1,2,3]
Output: 1
Explanation:
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1
Example 2:
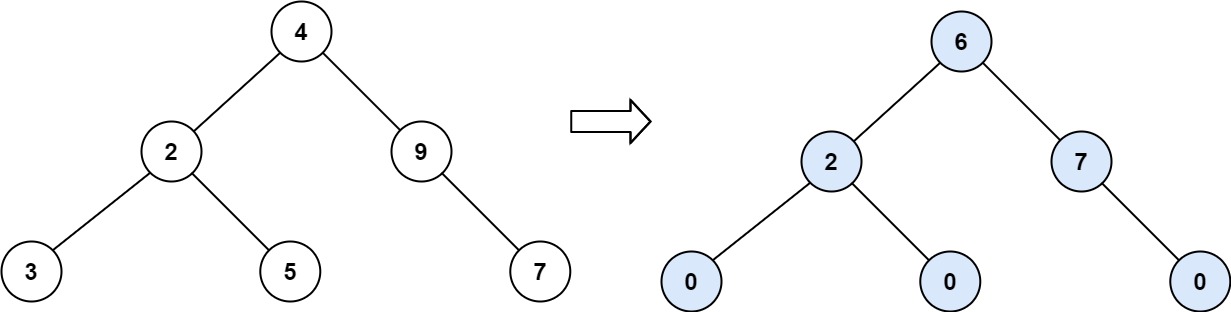
Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation:
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15
Constraints
- The number of nodes in the tree is in the range [0, ].
1000 <= Node.val <= 1000
Solution for Binary Tree Tilt
Overview
First of all, let us clarify the concept of tilt for a given node in a tree.
In order to calculate the tilt value for a node, we need to know the sum of nodes in its left and right subtrees respectively.
Assume that we have a function valueSum(node) which gives the sum of all nodes, starting from the input node, then the sum of the node's left subtree would be valueSum(node.left).
Similarly, the sum of its right subtree would be valueSum(node.right).
With the above functions, we can then define the tilt value of a node as follows:
Given the above formula, we show an example on how the tilt value of each node looks like, in the following graph:
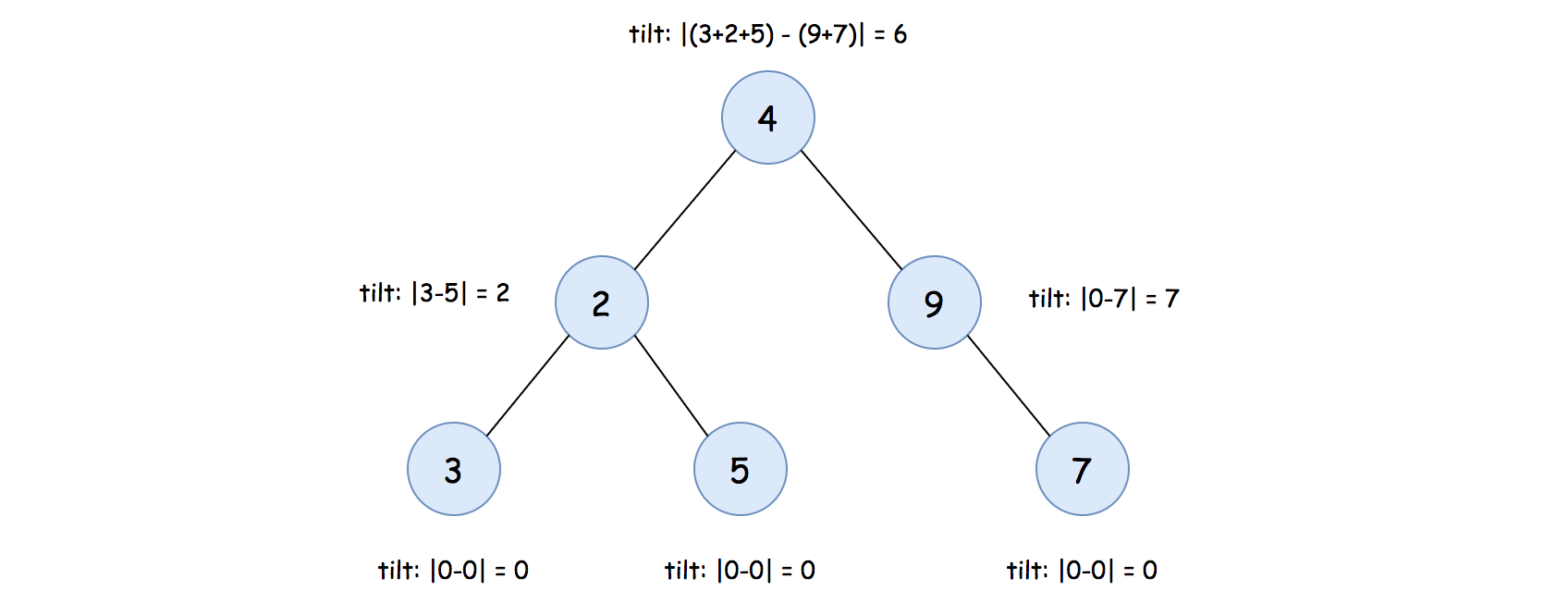 Note: when a subtree is empty, its value sum is zero.
As a result, the tilt value for a leaf node would be zero, since both the left and right subtree of a leaf node are empty.
Note: when a subtree is empty, its value sum is zero.
As a result, the tilt value for a leaf node would be zero, since both the left and right subtree of a leaf node are empty.
Approach 1: Post-Order DFS Traversal
Intuition
The overall idea is that we traverse each node, and calculate the tilt value for each node. At the end, we sum up all the tilt values, which is the desired result of the problem.
There are in general two strategies to traverse a tree data structure, namely Breadth-First Search (BFS) and Depth-First Search (DFS).
Concerning the DFS strategy, it can further be divided into three categories: Pre-Order, In-Order and Post-Order, depending on the relative order of visit among the node and its children nodes.
Sometimes, both strategies could work for a specific problem. In other cases, one of them might be more adapted to the problem. In our case here, the DFS is a more optimized choice, as one will see later. More specifically, we could apply the Post-Order DFS traversal here.
Algorithm
As we discussed before, in order to calculate the tilt value for a node, we need to calculate the sum of its left and right subtrees respectively.
Let us first implement the function valueSum(node) which returns the sum of values for all nodes starting from the given node, which can be summarized with the following recursive formula:
Furthermore, the tilt value of a node also depends on the value sum of its left and right subtrees, as follows:
Intuitively, we could combine the above calculations within a single recursive function. In this way, we only need to traverse each node once and only once.
More specifically, we will traverse the tree in the post-order DFS, i.e. we visit a node's left and right subtrees before processing the value of the current node.
Code in Different Languages
- C++
- Java
- Python
#include <cmath>
class Solution {
private:
int totalTilt;
int valueSum(TreeNode* node) {
if (node == nullptr)
return 0;
int leftSum = valueSum(node->left);
int rightSum = valueSum(node->right);
int tilt = std::abs(leftSum - rightSum);
totalTilt += tilt;
return node->val + leftSum + rightSum;
}
public:
int findTilt(TreeNode* root) {
totalTilt = 0;
valueSum(root);
return totalTilt;
}
};
class Solution {
private int totalTilt = 0;
protected int valueSum(TreeNode node) {
if (node == null)
return 0;
int leftSum = this.valueSum(node.left);
int rightSum = this.valueSum(node.right);
int tilt = Math.abs(leftSum - rightSum);
this.totalTilt += tilt;
// return the sum of values starting from this node.
return node.val + leftSum + rightSum;
}
public int findTilt(TreeNode root) {
this.totalTilt = 0;
this.valueSum(root);
return this.totalTilt;
}
}
class Solution:
def findTilt(self, root: TreeNode) -> int:
total_tilt = 0
def valueSum(node):
nonlocal total_tilt
if not node:
return 0
left_sum = valueSum(node.left)
right_sum = valueSum(node.right)
tilt = abs(left_sum - right_sum)
total_tilt += tilt
return left_sum + right_sum + node.val
valueSum(root)
return total_tilt
Complexity Analysis
Time Complexity:
Reason: We traverse each node once and only once. During the traversal, we calculate the tilt value for each node.
Space Complexity:
Reason:
Although the variables that we used in the algorithm are of constant-size, we applied recursion in the algorithm which incurs additional memory consumption in function call stack.
In the worst case where the tree is not well balanced, the recursion could pile up N times. As a result, the space complexity of the algorithm is O(N).
References
-
LeetCode Problem: Binary Tree Tilt
-
Solution Link: Binary Tree Tilt