Out of Boundary Paths
Problem Description
There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.
Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo .
Examples
Example 1:
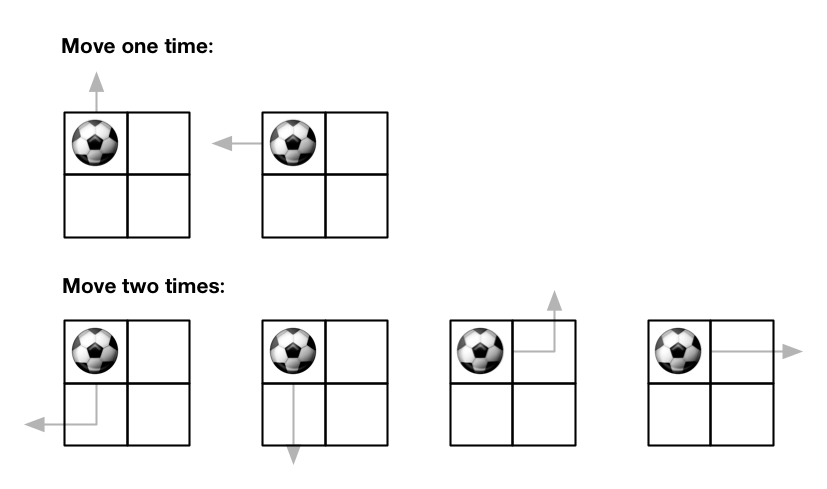
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output: 6
Example 2:
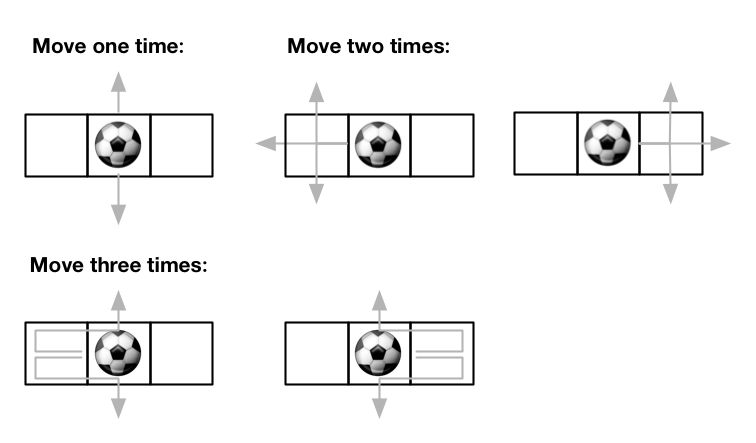
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output: 12
Constraints
1 <= m, n <= 500 <= maxMove <= 500 <= startRow < m0 <= startColumn < n
Solution for Out of Boundary Paths
Approach 1: Brute Force [Time Limit Exceeded]
Algorithm
In the brute force approach, we try to take one step in every direction and decrement the number of pending moves for each step taken. Whenever we reach out of the boundary while taking the steps, we deduce that one extra path is available to take the ball out.
In order to implement the same, we make use of a recursive function findPaths(m,n,N,i,j) which takes the current number of moves(N) along with the current position(i,j) as some of the parameters and returns the number of moves possible to take the ball out with the current pending moves from the current position. Now, we take a step in every direction and update the corresponding indices involved along with the current number of pending moves.
Further, if we run out of moves at any moment, we return a 0 indicating that the current set of moves doesn't take the ball out of boundary.
Code in Different Languages�
- C++
- Java
- Python
class Solution {
public:
int findPaths(int m, int n, int N, int i, int j) {
if (i == m || j == n || i < 0 || j < 0) return 1;
if (N == 0) return 0;
return findPaths(m, n, N - 1, i - 1, j)
+ findPaths(m, n, N - 1, i + 1, j)
+ findPaths(m, n, N - 1, i, j - 1)
+ findPaths(m, n, N - 1, i, j + 1);
}
};
class Solution {
public int findPaths(int m, int n, int N, int i, int j) {
if (i == m || j == n || i < 0 || j < 0) return 1;
if (N == 0) return 0;
return findPaths(m, n, N - 1, i - 1, j)
+ findPaths(m, n, N - 1, i + 1, j)
+ findPaths(m, n, N - 1, i, j - 1)
+ findPaths(m, n, N - 1, i, j + 1);
}
}
class Solution:
def findPaths(self, m: int, n: int, N: int, i: int, j: int) -> int:
if i == m or j == n or i < 0 or j < 0:
return 1
if N == 0:
return 0
return (self.findPaths(m, n, N - 1, i - 1, j) +
self.findPaths(m, n, N - 1, i + 1, j) +
self.findPaths(m, n, N - 1, i, j - 1) +
self.findPaths(m, n, N - 1, i, j + 1))
Complexity Analysis
Time Complexity:
Reason: Size of recursion tree will be . Here, N refers to the number of moves allowed.
Space Complexity:
Reason: The depth of the recursion tree can go upto N.
Approach 2: Recursion with Memoization
Algorithm
In the brute force approach, while going through the various branches of the recursion tree, we could reach the same position with the same number of moves left.
Thus, a lot of redundant function calls are made with the same set of parameters leading to a useless increase in runtime. We can remove this redundancy by making use of a memoization array, memo. memo[i][j][k] is used to store the number of possible moves leading to a path out of the boundary if the current position is given by the indices (i,j) and number of moves left is k.
Thus, now if a function call with some parameters is repeated, the memo array will already contain valid values corresponding to that function call resulting in pruning of the search space.
Code in Different Languages
- C++
- Java
- Python
#include <vector>
#include <cstring> // For memset
class Solution {
public:
int M = 1000000007;
int findPaths(int m, int n, int N, int i, int j) {
std::vector<std::vector<std::vector<int>>> memo(m, std::vector<std::vector<int>>(n, std::vector<int>(N + 1, -1)));
return findPaths(m, n, N, i, j, memo);
}
private:
int findPaths(int m, int n, int N, int i, int j, std::vector<std::vector<std::vector<int>>>& memo) {
if (i == m || j == n || i < 0 || j < 0) return 1;
if (N == 0) return 0;
if (memo[i][j][N] >= 0) return memo[i][j][N];
memo[i][j][N] = (
(findPaths(m, n, N - 1, i - 1, j, memo) + findPaths(m, n, N - 1, i + 1, j, memo)) % M +
(findPaths(m, n, N - 1, i, j - 1, memo) + findPaths(m, n, N - 1, i, j + 1, memo)) % M
) % M;
return memo[i][j][N];
}
};
class Solution {
int M = 1000000007;
public int findPaths(int m, int n, int N, int i, int j) {
int[][][] memo = new int[m][n][N + 1];
for (int[][] l : memo) for (int[] sl : l) Arrays.fill(sl, -1);
return findPaths(m, n, N, i, j, memo);
}
public int findPaths(int m, int n, int N, int i, int j, int[][][] memo) {
if (i == m || j == n || i < 0 || j < 0) return 1;
if (N == 0) return 0;
if (memo[i][j][N] >= 0) return memo[i][j][N];
memo[i][j][N] = (
(findPaths(m, n, N - 1, i - 1, j, memo) + findPaths(m, n, N - 1, i + 1, j, memo)) % M +
(findPaths(m, n, N - 1, i, j - 1, memo) + findPaths(m, n, N - 1, i, j + 1, memo)) % M
) % M;
return memo[i][j][N];
}
}
class Solution:
M = 1000000007
def findPaths(self, m: int, n: int, N: int, i: int, j: int) -> int:
memo = [[[-1 for _ in range(N + 1)] for _ in range(n)] for _ in range(m)]
return self.findPathsMemo(m, n, N, i, j, memo)
def findPathsMemo(self, m: int, n: int, N: int, i: int, j: int, memo: list) -> int:
if i == m or j == n or i < 0 or j < 0:
return 1
if N == 0:
return 0
if memo[i][j][N] >= 0:
return memo[i][j][N]
memo[i][j][N] = (
(self.findPathsMemo(m, n, N - 1, i - 1, j, memo) + self.findPathsMemo(m, n, N - 1, i + 1, j, memo)) % self.M +
(self.findPathsMemo(m, n, N - 1, i, j - 1, memo) + self.findPathsMemo(m, n, N - 1, i, j + 1, memo)) % self.M
) % self.M
return memo[i][j][N]
Complexity Analysis
Time Complexity:
Reason: We need to fill the memo array once with dimensions m×n×N. Here, m, n refer to the number of rows and columns of the given grid respectively. N refers to the total number of allowed moves.
Space Complexity:
Reason: memo array of size m×n×N is used.
References
-
LeetCode Problem: Out of Boundary Paths
-
Solution Link: Out of Boundary Paths