Find Largest Value in Each Tree Row
Problem Description
Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).
Examples
Example 1:
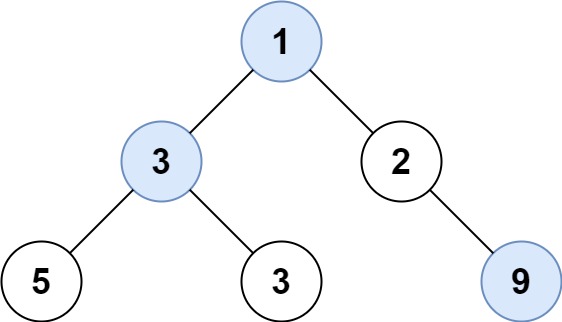
Input: root = [1,3,2,5,3,null,9]
Output: [1,3,9]
Example 2:
Input: root = [1,2,3]
Output: [1,3]
Constraints
- The number of nodes in the tree will be in the range .
Solution for Find Largest Value in Each Tree Row
Approach 1: Breadth First Search (BFS)
Intuition
BFS is perfect when we are dealing specifically with rows/levels of a binary tree. With BFS, we handle one row of the tree at a time.
Here, we need to find the maximum value in each row. We can simply perform a BFS and for each row, keep track of the maximum value we have seen so far. We will initialize an integer currMax to a small value like negative infinity. Then we go through the row and try to update currMax when we see larger values. After handling the row, we add currMax to our answer.
Algorithm
- If the
rootis null (empty) tree, just return an empty list. - Initialize the answer list
ansand aqueuewith therootto perform BFS. - Perform BFS - while the
queueis not empty:- Initialize
currMaxto a small value and save the length of the queue incurrentLength. - Iterate
currentLengthtimes:- Remove a
nodefrom thequeue. - Update
currMaxwithnode.valif it is larger. - For each child of
node, if it is not null, push it to thequeue.
- Remove a
- Add
currMaxtoans.
- Initialize
- Return ans.
Code in Different Languages
- C++
- Java
- Python
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
if (root == nullptr) {
return vector<int>{};
}
vector<int> ans;
queue<TreeNode*> queue;
queue.push(root);
while (!queue.empty()) {
int currentLength = queue.size();
int currMax = INT_MIN;
for (int i = 0; i < currentLength; i++) {
TreeNode* node = queue.front();
queue.pop();
currMax = max(currMax, node->val);
if (node->left) {
queue.push(node->left);
}
if (node->right) {
queue.push(node->right);
}
}
ans.push_back(currMax);
}
return ans;
}
};
class Solution {
public List<Integer> largestValues(TreeNode root) {
if (root == null) {
return new ArrayList<Integer>();
}
List<Integer> ans = new ArrayList<Integer>();
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
int currentLength = queue.size();
int currMax = Integer.MIN_VALUE;
for (int i = 0; i < currentLength; i++) {
TreeNode node = queue.remove();
currMax = Math.max(currMax, node.val);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
ans.add(currMax);
}
return ans;
}
}
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
ans = []
queue = deque([root])
while queue:
current_length = len(queue)
curr_max = float("-inf")
for _ in range(current_length):
node = queue.popleft()
curr_max = max(curr_max, node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
ans.append(curr_max)
return ans
Complexity Analysis
Time Complexity:
Reason: During the BFS, we visit each node in the tree once. At each node, we perform O(1) work.
Space Complexity:
Reason: In a perfect binary tree, the final row has nodes, all of which will be in
queue.
Approach 2: Depth First Search (DFS)
Intuition
In BFS, we handle each row explicitly, so it's easy to just keep track of the maximum value as we traverse through the row.
In DFS, the order in which we move through the tree is not related to the rows. Thus, we need to be more creative to find the maximum value in each row. The first observation to make is that each row can be described by the depth of its nodes.
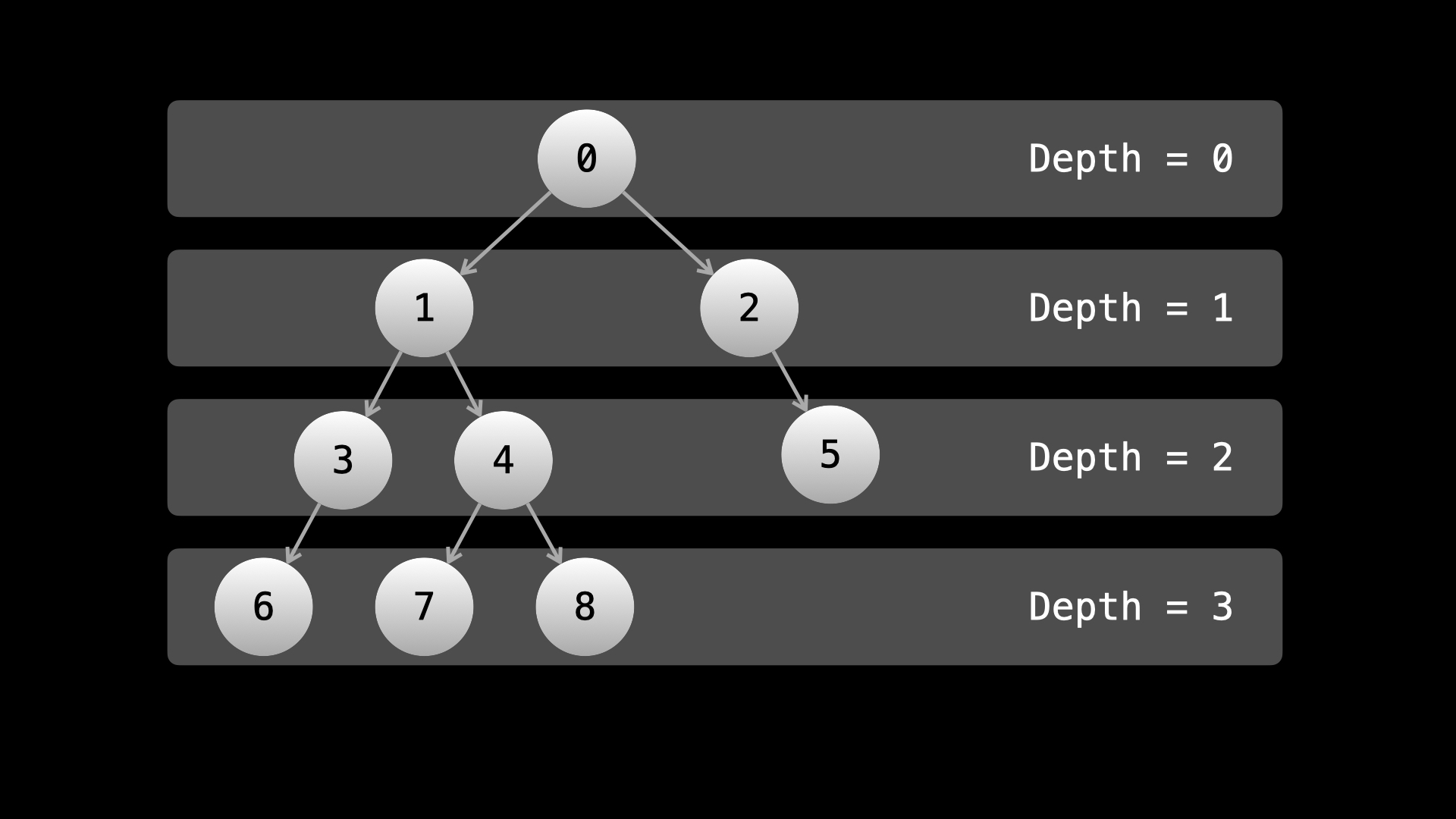
The depth of a node is its distance from the root. The root has a depth of 0, and every child has a depth of 1 greater than its parent. You may also notice that in terms of indices, each node's depth corresponds to its index in the answer.
For example, if ans is our answer list, then ans[2] holds the maximum value of all nodes with depth 2.
If we keep track of each node's depth during the traversal, then we can update ans directly. How do we keep track of the depth? We will pass an additional argument depth in our dfs function. When we initially call dfs with root, we will pass depth = 0. When we call dfs on a child, we will pass depth + 1.
There is one problem: how do we know what length ans should be? We will initialize ans as an empty list. If we are at a depth that would be out of bounds if we tried to access ans[depth], then we will simply initialize the current node.val as the maximum value seen at depth so far by pushing node.val to ans.
Algorithm
- Initialize ans as an empty list.
- Define a function dfs(node, depth):
- If node is null, return.
- If depth == ans.length, then push node.val to ans. Otherwise, try to update ans[depth] with node.val if its larger.
- Call dfs on node.left and node.right with depth + 1 as the second argument.
- Call dfs(root, 0) and then return ans.
Code in Different Languages
- C++
- Java
- Python
class Solution {
public:
vector<int> ans;
vector<int> largestValues(TreeNode* root) {
dfs(root, 0);
return ans;
}
void dfs(TreeNode* node, int depth) {
if (node == nullptr) {
return;
}
if (depth == ans.size()) {
ans.push_back(node->val);
} else {
ans[depth] = max(ans[depth], node->val);
}
dfs(node->left, depth + 1);
dfs(node->right, depth + 1);
}
};
class Solution {
List<Integer> ans;
public List<Integer> largestValues(TreeNode root) {
ans = new ArrayList<Integer>();
dfs(root, 0);
return ans;
}
public void dfs(TreeNode node, int depth) {
if (node == null) {
return;
}
if (depth == ans.size()) {
ans.add(node.val);
} else {
ans.set(depth, Math.max(ans.get(depth), node.val));
}
dfs(node.left, depth + 1);
dfs(node.right, depth + 1);
}
}
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[int]:
def dfs(node, depth):
if not node:
return
if depth == len(ans):
ans.append(node.val)
else:
ans[depth] = max(ans[depth], node.val)
dfs(node.left, depth + 1)
dfs(node.right, depth + 1)
ans = []
dfs(root, 0)
return ans
Complexity Analysis
Time Complexity:
Reason: During the DFS, we visit each node in the tree once. At each node, we perform O(1) work.
Space Complexity:
Reason: We use extra space for the recursion call stack. The most calls in the call stack at any given time will be the max depth of the tree. In the worst-case scenario where the tree is like a linked list, the max depth will be O(N).
Approach 3: DFS, Iterative
Intuition
We can also implement DFS iteratively using a stack. Each entry in the stack will be a pair node, depth. We will use a while loop to perform the DFS, with each iteration being analogous to a function call from the previous approach. As such, we will perform the same process in each while loop iteration: try to update ans with node.val, then push the children of node to the stack if they exist.
Algorithm
- If the
rootis null (empty) tree, just return an empty list. - Initialize the answer list
ansand astackwith(root, 0). - While the
stackis not empty:- Pop
(node, depth)from the stack. - If
depth == ans.length, then pushnode.valtoans. Otherwise, try to updateans[depth]withnode.valif its larger. - If
node.leftis not null, push(node.left, depth + 1)tostack. - If
node.rightis not null, push(node.right, depth + 1)tostack.
- Pop
- Return
ans.
Code in Different Languages
- C++
- Java
- Python
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
if (root == nullptr) {
return vector<int>{};
}
vector<int> ans;
stack<pair<TreeNode*, int>> stack;
stack.push(make_pair(root, 0));
while (!stack.empty()) {
pair<TreeNode*, int> pair = stack.top();
stack.pop();
TreeNode* node = pair.first;
int depth = pair.second;
if (depth == ans.size()) {
ans.push_back(node->val);
} else {
ans[depth] = max(ans[depth], node->val);
}
if (node->left) {
stack.push(make_pair(node->left, depth + 1));
}
if (node->right) {
stack.push(make_pair(node->right, depth + 1));
}
}
return ans;
}
};
class Solution {
public List<Integer> largestValues(TreeNode root) {
if (root == null) {
return new ArrayList<Integer>();
}
List<Integer> ans = new ArrayList<>();
Stack<Pair<TreeNode, Integer>> stack = new Stack<>();
stack.push(new Pair<>(root, 0));
while (!stack.isEmpty()) {
Pair<TreeNode, Integer> pair = stack.pop();
TreeNode node = pair.getKey();
int depth = pair.getValue();
if (depth == ans.size()) {
ans.add(node.val);
} else {
ans.set(depth, Math.max(ans.get(depth), node.val));
}
if (node.left != null) {
stack.push(new Pair<>(node.left, depth + 1));
}
if (node.right != null) {
stack.push(new Pair<>(node.right, depth + 1));
}
}
return ans;
}
}
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
ans = []
stack = [(root, 0)]
while stack:
node, depth = stack.pop()
if depth == len(ans):
ans.append(node.val)
else:
ans[depth] = max(ans[depth], node.val)
if node.left:
stack.append((node.left, depth + 1))
if node.right:
stack.append((node.right, depth + 1))
return ans
Complexity Analysis
Time Complexity:
Reason: During the DFS, we visit each node in the tree once. At each node, we perform O(1) work.
Space Complexity:
Reason: We use extra space for the recursion call stack. The most calls in the call stack at any given time will be the max depth of the tree. In the worst-case scenario where the tree is like a linked list, the max depth will be O(N).
We pop the top node from the stack and then push its child nodes onto the stack based on the DFS traversal strategy. This process of pushing and popping forms a path-like structure within the stack, and the length of this path will not exceed the height of the tree. Therefore, O(H) space will be used.
References
-
LeetCode Problem: Find Largest Value in Each Tree Row
-
Solution Link: Find Largest Value in Each Tree Row