Sum root to leaf numbers
Problem Statement
You are given the root of a binary tree containing digits from 0 to 9 only.
Each root-to-leaf path in the tree represents a number.
For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.
Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.
A leaf node is a node with no children
Examples
Example 1:
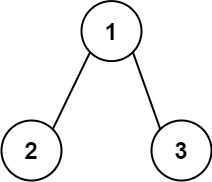
Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.
Example 2:
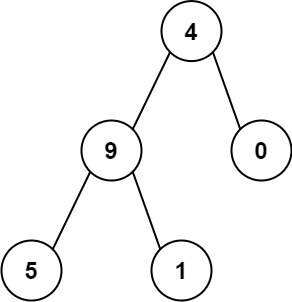
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.
Constraints
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 9The depth of the tree will not exceed 10.
Solution
Intuition
The intuition behind this solution is to perform a level-order traversal of the binary tree using a queue. While traversing the tree level by level, we keep track of the current sum along the path from the root to each node. When we encounter a leaf node, we add its corresponding sum to the total sum of all root-to-leaf numbers.
Approach
- Initialize a total sum variable to keep track of the sum of all root-to-leaf numbers.
- Initialize two queues: one for storing the tree nodes and another for storing the corresponding sums.
- Enqueue the root node and its value into the respective queues.
- While there are nodes in the queue, dequeue a node and its corresponding sum.
- If the dequeued node is a leaf node, add its sum to the total sum.
- If the dequeued node has left or right children, enqueue them along with their corresponding sums (formed by appending the child node’s value to the current sum multiplied by 10).
- Repeat steps 4-6 until the queue is empty.
- Return the total sum.
C++
class Solution {
private:
int totalSum = 0;
void findSum(TreeNode* root, int currNum) {
if (root == nullptr) return;
if (root->left == nullptr && root->right == nullptr)
totalSum += (currNum * 10 + root->val);
currNum = currNum * 10 + root->val;
findSum(root->left, currNum);
findSum(root->right, currNum);
}
public:
int sumNumbers(TreeNode* root) {
findSum(root, 0);
return totalSum;
}
};
Java
class Solution {
private int totalSum = 0;
public int sumNumbers(TreeNode root) {
findSum(root, 0);
return totalSum;
}
private void findSum(TreeNode root, int currNum){
if(root == null) return;
if(root.left == null && root.right == null) totalSum += (currNum * 10 + root.val);
currNum = currNum * 10 + root.val;
findSum(root.left, currNum);
findSum(root.right, currNum);
}
}
Conclusion
Complexity
-
Time complexity: Since we visit each node exactly once, the time complexity is O(n), where n is the number of nodes in the binary tree.
-
Space complexity: In the worst case, when the tree is a complete binary tree, both queues can hold up to O(n/2) nodes, resulting in O(n) space complexity. However, in the average case, the space complexity is O(sqrt(n)), where n is the number of nodes in the binary tree.