Binary Tree Maximum path sum
Problem Description
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the root of a binary tree, return the maximum path sum of any non-empty path.
Examples
Example 1:
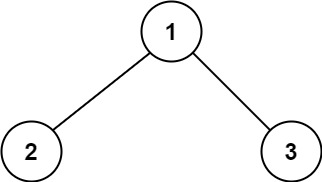
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Example 2:
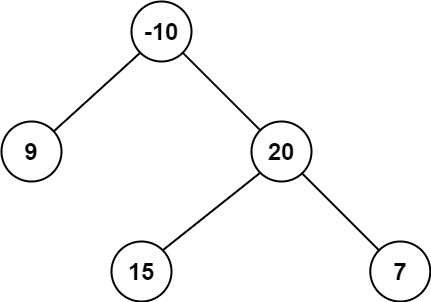
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Constraints
- The number of nodes in the tree is in the range .
1000 <= Node.val <= 1000
Solution
Intuition
Imagine you're an explorer in a magical forest (a binary tree). Each node of the tree is a treasure chest with some gold coins (node values). You want to find the path that gives you the maximum amount of gold. However, you can only travel down the tree, not back up, and you want to maximize your treasure by possibly starting and ending at any node.
Approach�
Here's how you, the explorer, will find the path with the most gold:
Explore and Collect Gold
At each treasure chest (node), you decide whether to collect gold from the left path, the right path, or both.
Maximize Gold
As you collect gold from each path, you keep track of the maximum treasure you've found so far.
Avoid Negative Gold
If a path leads to a loss (negative value), you pretend it’s zero to avoid losing your precious gold.
Step-by-Step Plan
-
Recursive Function
- Use a helper function that returns the maximum gold you can collect starting from any node downwards.
-
Track Max Sum
- As you calculate the maximum gold from the left and right paths, update the global maximum if the total gold from the current node (including left and right paths) is higher.
-
Return Path Sum
- For each node, return the maximum gold that can be collected starting from that node and going down one path (either left or right).
Code in Different languages
Code in C++
class Solution {
public:
int pathsum(TreeNode* root, int &max_sum){
if(root == nullptr) return 0;
int l_sum = max(0, pathsum(root->left, max_sum));
int r_sum = max(0, pathsum(root->right, max_sum));
max_sum = max(max_sum, root->val + l_sum + r_sum);
return root->val + max(l_sum , r_sum);
}
int maxPathSum(TreeNode* root) {
int max_sum = INT_MIN;
pathsum(root, max_sum);
return max_sum;
}
};
class Solution:
def maxPathSum(self, root: Optional[TreeNode]) -> int:
res = root.val
def dfs(node):
nonlocal res
if not node: return 0
leftMax = dfs(node.left)
rightMax = dfs(node.right)
leftMax = max(leftMax, 0)
rightMax = max(rightMax, 0)
res = max(res, node.val + leftMax + rightMax)
return node.val + max(leftMax , rightMax)
dfs(root)
return res
Complexity
-
Time complexity:
-
Space complexity: