Balanced Binary Tree Solution

Problem Description

Given a binary tree, determine if it is height-balanced.

A height-balanced binary tree is defined as:

• A binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Examples

Example 1:

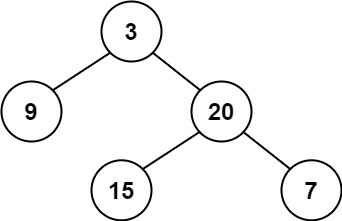
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

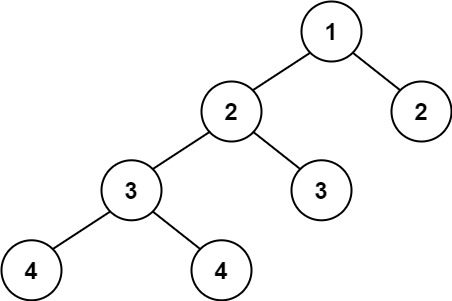
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

Constraints

• The number of nodes in the tree is in the range [0, 5000].
• $-10^4 <=$ Node.val $<= 10^4$

---

Solution for Balanced Binary Tree Problem

• Recursive
• Bottom-Up

Approach 1: Top-Down

Intuition

This method checks whether the tree is balanced strictly according to the definition of a balanced binary tree: the difference between the heights of the two subtrees is not greater than 1, and both the left and right subtrees are also balanced. With the helper function depth(), we can easily write the code.

Implementation

Implement a helper function depth(root) that returns the depth of the tree rooted at root. Check if the absolute difference between the depths of the left and right subtrees is not greater than 1. Recursively check if both the left and right subtrees are balanced. Return true if the tree is balanced, otherwise return false.

Code in Different Languages

Java

Written by @Vipullakum007

 class Solution {
     public int depth(TreeNode root) {
         if (root == null) return 0;
         return Math.max(depth(root.left), depth(root.right)) + 1;
     }

     public boolean isBalanced(TreeNode root) {
         if (root == null) return true;

         int left = depth(root.left);
         int right = depth(root.right);

         return Math.abs(left - right) <= 1 && isBalanced(root.left) && isBalanced(root.right);
     }
 }

Python

Written by @Vipullakum007

 class Solution:
     def depth(self, root: TreeNode) -> int:
         if root is None:
             return 0
         return max(self.depth(root.left), self.depth(root.right)) + 1

     def isBalanced(self, root: TreeNode) -> bool:
         if root is None:
             return True

         left = self.depth(root.left)
         right = self.depth(root.right)

         return abs(left - right) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)

C++

Written by @Vipullakum007

 class Solution {
 public:
     int depth(TreeNode* root) {
         if (root == nullptr) return 0;
         return max(depth(root->left), depth(root->right)) + 1;
     }

     bool isBalanced(TreeNode* root) {
         if (root == nullptr) return true;

         int left = depth(root->left);
         int right = depth(root->right);

         return abs(left - right) <= 1 && isBalanced(root->left) && isBalanced(root->right);
     }
 };

Complexity Analysis

• Time Complexity: O(n log n) in the worst case where n is the number of nodes in the tree. We visit each node once, and for each node, we calculate its depth. Since the depth calculation involves traversing the subtree, the overall time complexity is O(n log n).
• Space Complexity: O(n) for the recursive call stack.

References

• LeetCode Problem: Balanced Binary Tree
• Solution Link: LeetCode Solution
• Authors GeeksforGeeks Profile: Vipul lakum

---