Clone graph
Problem Description
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}
Test case format:
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Examples
Example 1:
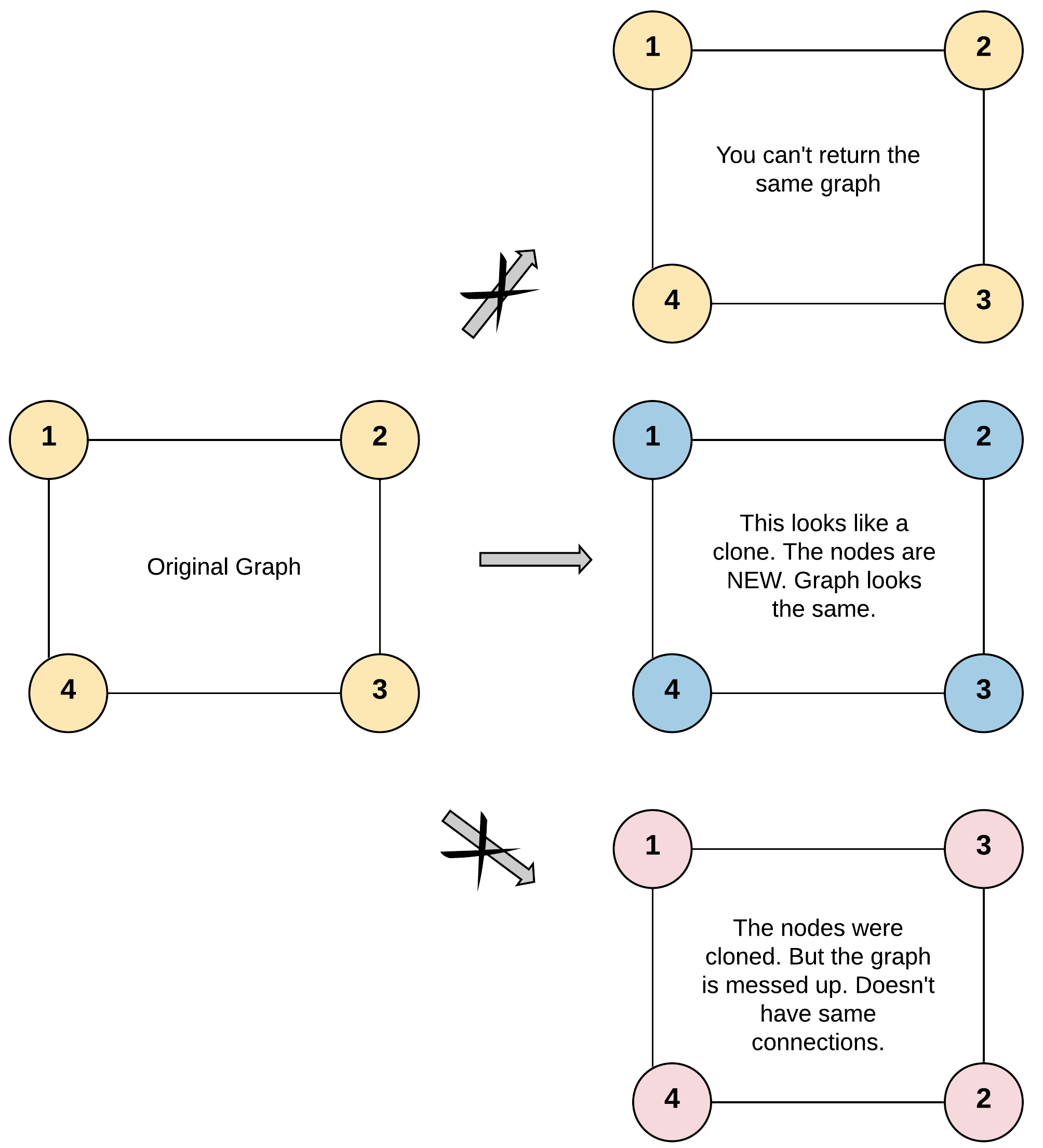
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
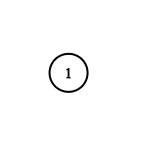
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.
Constraints
- The number of nodes in the graph is in the range
[0, 100]. 1 <= Node.val <= 100- Node.val is unique for each node.
- There are no repeated edges and no self-loops in the graph.
- The Graph is connected and all nodes can be visited starting from the given node.
Intuition
Use a Depth-First Search (DFS) approach to traverse the original graph. During the traversal:
- Create a new node for each encountered node and maintain a mapping between the original nodes and their corresponding clones.
- When processing a node's neighbors, check if the clone of the neighbor has already been created. If so, use the clone from the mapping; otherwise, recursively explore the neighbor to create its clone.
Approach
-
Define a Helper Function
dfs:The
dfsfunction performs the following tasks:- Parameters: Takes a node
curfrom the original graph and a mappingmpwhich stores the relationship between original nodes and their clones. - Steps:
- Create a New Node:
- Create a new clone node with the same value as
cur.
- Create a new clone node with the same value as
- Add Mapping:
- Add an entry in the mapping
mpto link the original nodecurwith the newly createdclone.
- Add an entry in the mapping
- Initialize Neighbors:
- Initialize an empty vector
neighbourto store the cloned neighbors ofcur.
- Initialize an empty vector
- Process Neighbors:
- Iterate through the neighbors of
cur:- If the Neighbor is Already Cloned: If
mp.find(it) != mp.end(), use the clone from the mapping. - If the Neighbor is Not Cloned: Recursively call
dfson the neighbor to get its clone.
- If the Neighbor is Already Cloned: If
- Iterate through the neighbors of
- Set Neighbors:
- Set the
neighboursof thecloneto theneighbourvector.
- Set the
- Return Clone:
- Return the
clone.
- Return the
- Create a New Node:
- Parameters: Takes a node
-
Define the
cloneGraphFunction:This function initializes the cloning process:
- Steps:
- Initialize the Mapping:
- Create an unordered map
mpto store the mapping between original nodes and their clones.
- Create an unordered map
- Check for Null Node:
- Check if the
nodeisNULL, and if so, returnNULL.
- Check if the
- Call
dfs:- Call the
dfsfunction with the original node and the mappingmp.
- Call the
- Initialize the Mapping:
- Steps:
Code in Different Languages
C++
class Solution {
public:
Node* dfs(Node* cur,unordered_map<Node*,Node*>& mp)
{
vector<Node*> neighbour;
Node* clone=new Node(cur->val);
mp[cur]=clone;
for(auto it:cur->neighbors)
{
if(mp.find(it)!=mp.end()) //already in map
{
neighbour.push_back(mp[it]);
}
else
neighbour.push_back(dfs(it,mp));
}
clone->neighbors=neighbour;
return clone;
}
Node* cloneGraph(Node* node) {
unordered_map<Node*,Node*> mp;
if(node==NULL)
return NULL;
return dfs(node,mp);
}};
Java
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> neighbors;
public Node() {
val = 0;
neighbors = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new ArrayList<Node>();
}
public Node(int _val, ArrayList<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
}
*/
class Solution {
HashMap<Integer, Node> visited = new HashMap<>();
public Node cloneGraph(Node node) {
Node ans = new Node();
if(node == null){
return null;
}
ans.val = node.val;
visited.put(node.val, ans);
for(int i=0; i<node.neighbors.size(); i++){
if(!visited.containsKey(node.neighbors.get(i).val)){
cloneGraph(node.neighbors.get(i));
}
}
for(int i=0; i<node.neighbors.size(); i++){
ans.neighbors.add(visited.get(node.neighbors.get(i).val));
}
return ans;
}
}
Python
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
if not node: return node
q, clones = deque([node]), {node.val: Node(node.val, [])}
while q:
cur = q.popleft()
cur_clone = clones[cur.val]
for ngbr in cur.neighbors:
if ngbr.val not in clones:
clones[ngbr.val] = Node(ngbr.val, [])
q.append(ngbr)
cur_clone.neighbors.append(clones[ngbr.val])
return clones[node.val]
Complexity Analysis
-
Time Complexity: O(V + E)
- V is the number of nodes and E is the number of edges. The DFS traverses each node and edge once.
-
Space Complexity: O(V)
- Space is used for the mapping between nodes and their clones, which requires O(V) space.