Min Cost to Connect All Points
Problem Description
You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
Examples
Example 1:
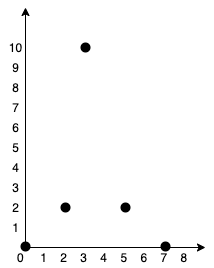
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation:

We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
Constraints
1 <= points.length <= 1000-10^6 <= xi, yi <= 10^6All pairs (xi, yi) are distinct.
Solution for Min Cost to Connect All Points
Approach
Prim's algorithm:
- Prim's algorithm is an algorithm for solving the optimization problem of finding the minimum spanning tree in a weighted connected graph within graph theory. A minimum spanning tree is a subset of the edges of the graph that forms a tree containing all vertices while minimizing the total weight of those edges.
Overview of the Algorithm:
- Calculate the distances between each pair of points and use Prim's algorithm to form the minimum spanning tree.
- Start from an initial point, mark it as visited, and select the point with the smallest distance among the unvisited points.
- Calculate the distances from the selected point to the unvisited points and store them in a cache.
- Add the minimum cost edge to the priority queue using the distances from the cache.
- Repeat the above steps until all points are visited, and calculate the minimum cost.
Specific Steps:��
Initial State:
- n: Number of points
- min_cost: Minimum cost (initially 0) and return value
- visited: A list to indicate if each point is visited (initially all False)
- pq: Priority queue (initially (0, 0) indicating starting from point 0 with cost 0)
- cache: Dictionary for caching distances (initially empty)
Each Step:
- Pop cost and point from pq (start from the initial point).
- If the point is already visited, skip this point.
- Otherwise, mark this point as visited and add the current cost to the minimum cost.
- Calculate distances from this point to all unvisited points and store them in the cache. Update the cache if the new distance is smaller.
- Add the point with the smallest distance among the unvisited points to the priority queue using distances from the cache.
- Repeat steps 3 to 5 until all points are visited.
- Return the final minimum cost.
- Solution
Implementation
Live Editor
function Solution(arr) { var minCostConnectPoints = function(points) { let cost = 0; const n = points.length; const dist = Array(n).fill(Infinity); dist[0] = 0; let next = 0; for (let step = 1; step < n; step++) { let min = Infinity; let point = -1; for (let i = 1; i < n; i++) { if (dist[i] > 0) { dist[i] = Math.min(dist[i], Math.abs(points[i][0] - points[next][0]) + Math.abs(points[i][1] - points[next][1])); if (dist[i] < min) { min = dist[i]; point = i; } } } cost += min; dist[point] = 0; next = point; } return cost; }; const input = [[0,0],[2,2],[3,10],[5,2],[7,0]] const output =minCostConnectPoints(input) return ( <div> <p> <b>Input: </b> {JSON.stringify(input)} </p> <p> <b>Output:</b> {output.toString()} </p> </div> ); }
Result
Loading...
Complexity Analysis
- Time Complexity:
- Space Complexity:
Code in Different Languages
- JavaScript
- TypeScript
- Python
- Java
- C++
manhattDist(v1, v2) {
return Math.abs(v1[0] - v2[0]) + Math.abs(v1[1] - v2[1]);
}
minCostConnectPoints(points) {
const n = points.length;
const adj = Array.from({ length: n }, () => []);
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
const dist = this.manhattDist(points[i], points[j]);
adj[i].push([j, dist]);
adj[j].push([i, dist]);
}
}
const pq = new MinPriorityQueue({ priority: x => x[0] });
const vis = Array(n).fill(false);
pq.enqueue([0, 0]);
let cost = 0;
while (!pq.isEmpty()) {
const [topEdgwWt, currNode] = pq.dequeue().element;
if (vis[currNode]) continue;
vis[currNode] = true;
cost += topEdgwWt;
for (const [adjPoint, edWt] of adj[currNode]) {
if (!vis[adjPoint]) {
pq.enqueue([edWt, adjPoint]);
}
}
}
return cost;
}
class Solution {
manhattDist(v1: number[], v2: number[]): number {
return Math.abs(v1[0] - v2[0]) + Math.abs(v1[1] - v2[1]);
}
minCostConnectPoints(points: number[][]): number {
const n = points.length;
const adj: [number, number][][] = Array.from({ length: n }, () => []);
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
const dist = this.manhattDist(points[i], points[j]);
adj[i].push([j, dist]);
adj[j].push([i, dist]);
}
}
const pq = new MinPriorityQueue({ priority: (x: [number, number]) => x[0] });
const vis = Array(n).fill(false);
pq.enqueue([0, 0]);
let cost = 0;
while (!pq.isEmpty()) {
const [topEdgwWt, currNode] = pq.dequeue().element;
if (vis[currNode]) continue;
vis[currNode] = true;
cost += topEdgwWt;
for (const [adjPoint, edWt] of adj[currNode]) {
if (!vis[adjPoint]) {
pq.enqueue([edWt, adjPoint]);
}
}
}
return cost;
}
}
import heapq
class Solution:
def manhattDist(self, v1, v2):
return abs(v1[0] - v2[0]) + abs(v1[1] - v2[1])
def minCostConnectPoints(self, points):
n = len(points)
adj = [[] for _ in range(n)]
for i in range(n):
for j in range(i + 1, n):
dist = self.manhattDist(points[i], points[j])
adj[i].append((j, dist))
adj[j].append((i, dist))
pq = [(0, 0)] # (distance, point)
vis = [False] * n
cost = 0
while pq:
topEdgwWt, currNode = heapq.heappop(pq)
if vis[currNode]:
continue
vis[currNode] = True
cost += topEdgwWt
for adjPoint, edWt in adj[currNode]:
if not vis[adjPoint]:
heapq.heappush(pq, (edWt, adjPoint))
return cost
import java.util.*;
class Solution {
private int manhattDist(int[] v1, int[] v2) {
return Math.abs(v1[0] - v2[0]) + Math.abs(v1[1] - v2[1]);
}
public int minCostConnectPoints(int[][] points) {
int n = points.length;
List<List<int[]>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int dist = manhattDist(points[i], points[j]);
adj.get(i).add(new int[]{j, dist});
adj.get(j).add(new int[]{i, dist});
}
}
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
boolean[] vis = new boolean[n];
pq.add(new int[]{0, 0}); // {distance, point}
int cost = 0;
while (!pq.isEmpty()) {
int[] curr = pq.poll();
int topEdgwWt = curr[0];
int currNode = curr[1];
if (vis[currNode]) continue;
vis[currNode] = true;
cost += topEdgwWt;
for (int[] neighbor : adj.get(currNode)) {
int adjPoint = neighbor[0];
int edWt = neighbor[1];
if (!vis[adjPoint]) {
pq.add(new int[]{edWt, adjPoint});
}
}
}
return cost;
}
}
class Solution {
public:
int manhattDist(vector<int>&v1 , vector<int>&v2)
{
return abs(abs(v1[0]-v2[0]) + abs(v1[1]-v2[1]));
}
int minCostConnectPoints(vector<vector<int>>& points) {
int n = points.size();
vector<pair<int,int>> adj[n]; //{point , cost or Manhattan dist}
//we have to make a adjacency list fom every point to every other point
for(int i=0; i<n ; i++)
{
for(int j=i+1;j<n ; j++)
{
adj[i].push_back({j , manhattDist(points[i] , points[j])});
adj[j].push_back({i , manhattDist(points[i] , points[j])});
}
}
priority_queue<pair<int,int> , vector<pair<int,int>> , greater<pair<int,int>> > pq;
// {distance , point}
vector<int> vis(n,0);
pq.push({0,0}); //starting from 0 as source
int Cost=0;
while(!pq.empty())
{
auto it = pq.top();
pq.pop();
int CurrNode = it.second ;
int topEdgwWt = it.first;
if(vis[CurrNode]==1) continue;
vis[CurrNode]=1;
Cost+=topEdgwWt;
for(auto it: adj[CurrNode])
{
int adjPoint=it.first;
int edWt=it.second;
if(!vis[adjPoint])
{
pq.push({edWt , adjPoint});
}
}
}
return Cost;
}
};
References
-
LeetCode Problem: Min Cost to Connect All Points
-
Solution Link: LeetCode Solution