Magnetic Force Between Two Balls
Problem Description
In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the ith basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.
Rick stated that magnetic force between two different balls at positions x and y is |x - y|.
Given the integer array position and the integer m. Return the required force.
Examples
Example 1:
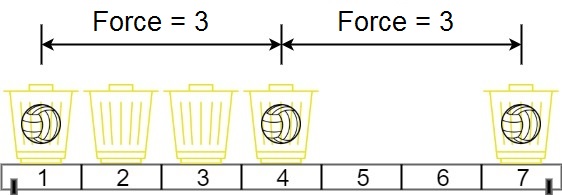
Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
Constraints
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9All integers in position are distinct.2 <= m <= position.length
Solution for Min Cost to Connect All Points
Approach
To solve this problem, we can utilize a binary search algorithm combined with a greedy approach. The goal is to determine the largest minimum distance possible between any two balls. Here's the step-by-step approach:
- Sorting: First, sort the positions array. This will help in easily calculating the distance between consecutive positions.
- Binary Search Setup:
- Initialize the search range for the possible distances. The lower bound (
low) is set to 1 (the smallest possible distance) and the upper bound (high) is set to the difference between the maximum and minimum positions (the largest possible distance).
- Initialize the search range for the possible distances. The lower bound (
- Binary Search Execution:
- While
lowis less than or equal tohigh, calculate the middle value (mid) of the current search range. - Use a helper function
possibleto check if it is possible to place allmballs such that the minimum distance between any two balls is at leastmid.- This is done by placing the first ball at the first position and then trying to place each subsequent ball at the next position that is at least
middistance away from the last placed ball. - If it is possible to place all
mballs in this manner, it meansmidis a valid candidate for the largest minimum distance, so we update the result and try for a larger distance by settinglowtomid + 1. - If it is not possible, it means
midis too large, so we try a smaller distance by settinghightomid - 1.
- This is done by placing the first ball at the first position and then trying to place each subsequent ball at the next position that is at least
- While
- Result: The largest valid
midfound during the binary search is the answer.
- Solution
Implementation
function Solution(arr) { function possible(position, m, mid) { let prev = position[0]; let cnt = 1; for (let i = 1; i < position.length; i++) { if (Math.abs(position[i] - prev) >= mid) { cnt++; prev = position[i]; } if (cnt >= m) return true; } return false; } function maxDistance(position, m) { position.sort((a, b) => a - b); let low = 1; let high = position[position.length - 1] - position[0]; let maxi = 0; while (low <= high) { let mid = Math.floor(low + (high - low) / 2); if (possible(position, m, mid)) { maxi = mid; low = mid + 1; } else { high = mid - 1; } } return maxi; } const input = [1,2,3,4,7], m = 3 const output = maxDistance(input , m) return ( <div> <p> <b>Input: </b> {JSON.stringify(input)} </p> <p> <b>Output:</b> {output.toString()} </p> </div> ); }
Complexity Analysis
- Time Complexity:
- Space Complexity:
Code in Different Languages
- JavaScript
- TypeScript
- Python
- Java
- C++
class Solution {
possible(position, m, mid) {
let prev = position[0];
let cnt = 1;
for (let i = 1; i < position.length; i++) {
if (Math.abs(position[i] - prev) >= mid) {
cnt++;
prev = position[i];
}
if (cnt >= m) return true;
}
return false;
}
maxDistance(position, m) {
position.sort((a, b) => a - b);
let low = 1;
let high = position[position.length - 1] - position[0];
let maxi = 0;
while (low <= high) {
let mid = Math.floor(low + (high - low) / 2);
if (this.possible(position, m, mid)) {
maxi = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return maxi;
}
}
class Solution {
possible(position: number[], m: number, mid: number): boolean {
let prev = position[0];
let cnt = 1;
for (let i = 1; i < position.length; i++) {
if (Math.abs(position[i] - prev) >= mid) {
cnt++;
prev = position[i];
}
if (cnt >= m) return true;
}
return false;
}
maxDistance(position: number[], m: number): number {
position.sort((a, b) => a - b);
let low = 1;
let high = position[position.length - 1] - position[0];
let maxi = 0;
while (low <= high) {
let mid = Math.floor(low + (high - low) / 2);
if (this.possible(position, m, mid)) {
maxi = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return maxi;
}
}
class Solution:
def possible(self, position, m, mid):
prev = position[0]
cnt = 1
for i in range(1, len(position)):
if abs(position[i] - prev) >= mid:
cnt += 1
prev = position[i]
if cnt >= m:
return True
return False
def maxDistance(self, position, m):
position.sort()
low, high = 1, position[-1] - position[0]
maxi = 0
while low <= high:
mid = (low + high) // 2
if self.possible(position, m, mid):
maxi = mid
low = mid + 1
else:
high = mid - 1
return maxi
import java.util.Arrays;
public class Solution {
public boolean possible(int[] position, int m, int mid) {
int prev = position[0];
int cnt = 1;
for (int i = 1; i < position.length; i++) {
if (Math.abs(position[i] - prev) >= mid) {
cnt++;
prev = position[i];
}
if (cnt >= m) return true;
}
return false;
}
public int maxDistance(int[] position, int m) {
Arrays.sort(position);
int low = 1;
int high = position[position.length - 1] - position[0];
int maxi = 0;
while (low <= high) {
int mid = low + (high - low) / 2;
if (possible(position, m, mid)) {
maxi = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return maxi;
}
}
class Solution {
public:
bool possible(vector<int>& position, int m, int mid) {
int prev = position[0];
int cnt = 1;
for (int i = 1; i < position.size(); i++) {
if (abs(position[i] - prev) >= mid) {
cnt++;
prev = position[i];
}
if (cnt >= m) return true;
}
return false;
}
int maxDistance(vector<int>& position, int m) {
sort(position.begin(), position.end());
int low = 1;
int high = position.back() - position[0];
int maxi = 0;
while (low <= high) {
int mid = low + (high - low) / 2;
if (possible(position, m, mid)) {
maxi = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return maxi;
}
};
References
-
LeetCode Problem: Magnetic Force Between Two Balls
-
Solution Link: LeetCode Solution