Cherry Pickup
Problem Description
You are given an n x n grid representing a field of cherries, each cell is one of three possible integers.
0means the cell is empty, so you can pass through,1means the cell contains a cherry that you can pick up and pass through, or-1means the cell contains a thorn that blocks your way.
Return the maximum number of cherries you can collect by following the rules below:
- Starting at the position
(0, 0)and reaching(n - 1, n - 1)by moving right or down through valid path cells (cells with value0or1). - After reaching
(n - 1, n - 1), returning to(0, 0)by moving left or up through valid path cells. - When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell
0. - If there is no valid path between
(0, 0)and(n - 1, n - 1), then no cherries can be collected.
Examples
Example 1:
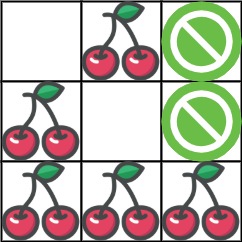
Input
["WordFilter", "f"]
[[["apple"]], ["a", "e"]]
Output
[null, 0]
Explanation
WordFilter wordFilter = new WordFilter(["apple"]);
wordFilter.f("a", "e"); // return 0, because the word at index 0 has prefix = "a" and suffix = "e".
Example 2:
Input: grid = [[1,1,-1],[1,-1,1],[-1,1,1]]
Output: 0
Constraints
n == grid.lengthn == grid[i].length1 <= n <= 50grid[i][j] is -1, 0, or 1.grid[0][0] != -1grid[n - 1][n - 1] != -1
Solution for Cherry Pickup
Approach 1: Dynamic Programming (Top Down)
Intuition
Instead of walking from end to beginning, let's reverse the second leg of the path, so we are only considering two paths from the beginning to the end.
Notice after t steps, each position (r, c) we could be, is on the line r + c = t. So if we have two people at positions (r1, c1) and (r2, c2), then r2 = r1 + c1 - c2. That means the variables r1, c1, c2 uniquely determine 2 people who have walked the same r1 + c1 number of steps. This sets us up for dynamic programming quite nicely.
Algorithm
Let dp[r1][c1][c2] be the most number of cherries obtained by two people starting at (r1, c1) and (r2, c2) and walking towards (N - 1, N - 1) picking up cherries, where r2 = r1 + c1 - c2.
If grid[r1][c1] and grid[r2][c2] are not thorns, then the value of dp[r1][c1][c2] is (grid[r1][c1] + grid[r2][c2]), plus the maximum of dp[r1 + 1][c1][c2], dp[r1][c1 + 1][c2], dp[r1 + 1][c1][c2 + 1], dp[r1][c1 + 1][c2 + 1] as appropriate. We should also be careful to not double count in case (r1, c1) == (r2, c2).
Why did we say it was the maximum of dp[r + 1][c1][c2] etc.? It corresponds to the 4 possibilities for persons 1 and 2 moving down and right:
- Person 1 down and person 2 down:
dp[r1 + 1][c1][c2]; - Person 1 right and person 2 down:
dp[r1][c1 + 1][c2]; - Person 1 down and person 2 right:
dp[r1 + 1][c1][c2 + 1]; - Person 1 right and person 2 right:
dp[r1][c1 + 1][c2 + 1];
Code in Different Languages
- C++
- Java
- Python
#include <vector>
#include <algorithm>
#include <climits>
class Solution {
private:
std::vector<std::vector<std::vector<int>>> memo;
std::vector<std::vector<int>> grid;
int N;
public:
int cherryPickup(std::vector<std::vector<int>>& grid) {
this->grid = grid;
N = grid.size();
memo = std::vector<std::vector<std::vector<int>>>(N, std::vector<std::vector<int>>(N, std::vector<int>(N, INT_MIN)));
return std::max(0, dp(0, 0, 0));
}
int dp(int r1, int c1, int c2) {
int r2 = r1 + c1 - c2;
if (N == r1 || N == r2 || N == c1 || N == c2 ||
grid[r1][c1] == -1 || grid[r2][c2] == -1) {
return -999999;
} else if (r1 == N - 1 && c1 == N - 1) {
return grid[r1][c1];
} else if (memo[r1][c1][c2] != INT_MIN) {
return memo[r1][c1][c2];
} else {
int ans = grid[r1][c1];
if (c1 != c2) {
ans += grid[r2][c2];
}
ans += std::max(std::max(dp(r1, c1 + 1, c2 + 1), dp(r1 + 1, c1, c2 + 1)),
std::max(dp(r1, c1 + 1, c2), dp(r1 + 1, c1, c2)));
memo[r1][c1][c2] = ans;
return ans;
}
}
};
class Solution {
int[][][] memo;
int[][] grid;
int N;
public int cherryPickup(int[][] grid) {
this.grid = grid;
N = grid.length;
memo = new int[N][N][N];
for (int[][] layer: memo) {
for (int[] row: layer) {
Arrays.fill(row, Integer.MIN_VALUE);
}
}
return Math.max(0, dp(0, 0, 0));
}
public int dp(int r1, int c1, int c2) {
int r2 = r1 + c1 - c2;
if (N == r1 || N == r2 || N == c1 || N == c2 ||
grid[r1][c1] == -1 || grid[r2][c2] == -1) {
return -999999;
} else if (r1 == N - 1 && c1 == N - 1) {
return grid[r1][c1];
} else if (memo[r1][c1][c2] != Integer.MIN_VALUE) {
return memo[r1][c1][c2];
} else {
int ans = grid[r1][c1];
if (c1 != c2) {
ans += grid[r2][c2];
}
ans += Math.max(Math.max(dp(r1, c1 + 1, c2 + 1), dp(r1 + 1, c1, c2 + 1)),
Math.max(dp(r1, c1 + 1, c2), dp(r1 + 1, c1, c2)));
memo[r1][c1][c2] = ans;
return ans;
}
}
}
class Solution(object):
def cherryPickup(self, grid):
N = len(grid)
memo = [[[None] * N for _1 in xrange(N)] for _2 in xrange(N)]
def dp(r1, c1, c2):
r2 = r1 + c1 - c2
if (N == r1 or N == r2 or N == c1 or N == c2 or
grid[r1][c1] == -1 or grid[r2][c2] == -1):
return float('-inf')
elif r1 == c1 == N-1:
return grid[r1][c1]
elif memo[r1][c1][c2] is not None:
return memo[r1][c1][c2]
else:
ans = grid[r1][c1] + (c1 != c2) * grid[r2][c2]
ans += max(dp(r1, c1 + 1, c2 + 1), dp(r1 + 1, c1, c2 + 1),
dp(r1, c1 + 1, c2), dp(r1 + 1, c1, c2))
memo[r1][c1][c2] = ans
return ans
return max(0, dp(0, 0, 0))
Complexity Analysis
Time Complexity:
Reason: where N is the length of grid. Our dynamic programming has states, and each state is calculated once.
Space Complexity:
Reason: the size of
memo.
Approach 2: Dynamic Programming (Bottom Up)
Intuition
Like in Approach 2, we have the idea of dynamic programming.
Say r1 + c1 = t is the t-th layer. Since our recursion only references the next layer, we only need to keep two layers in memory at a time.
Algorithm
At time t, let dp[c1][c2] be the most cherries that we can pick up for two people going from (0, 0) to (r1, c1) and (0, 0) to (r2, c2), where r1 = t-c1, r2 = t-c2. Our dynamic program proceeds similarly to Approach 2.
Code in Different Languages
- C++
- Java
- Python
#include <vector>
#include <algorithm>
#include <climits>
class Solution {
public:
int cherryPickup(std::vector<std::vector<int>>& grid) {
int N = grid.size();
std::vector<std::vector<int>> dp(N, std::vector<int>(N, INT_MIN));
dp[0][0] = grid[0][0];
for (int t = 1; t <= 2 * N - 2; ++t) {
std::vector<std::vector<int>> dp2(N, std::vector<int>(N, INT_MIN));
for (int i = std::max(0, t - (N - 1)); i <= std::min(N - 1, t); ++i) {
for (int j = std::max(0, t - (N - 1)); j <= std::min(N - 1, t); ++j) {
if (grid[i][t - i] == -1 || grid[j][t - j] == -1) {
continue;
}
int val = grid[i][t - i];
if (i != j) {
val += grid[j][t - j];
}
for (int pi = i - 1; pi <= i; ++pi) {
for (int pj = j - 1; pj <= j; ++pj) {
if (pi >= 0 && pj >= 0) {
dp2[i][j] = std::max(dp2[i][j], dp[pi][pj] + val);
}
}
}
}
}
dp = std::move(dp2);
}
return std::max(0, dp[N - 1][N - 1]);
}
};
class Solution {
public int cherryPickup(int[][] grid) {
int N = grid.length;
int[][] dp = new int[N][N];
for (int[] row: dp) {
Arrays.fill(row, Integer.MIN_VALUE);
}
dp[0][0] = grid[0][0];
for (int t = 1; t <= 2*N - 2; ++t) {
int[][] dp2 = new int[N][N];
for (int[] row: dp2) {
Arrays.fill(row, Integer.MIN_VALUE);
}
for (int i = Math.max(0, t - (N - 1)); i <= Math.min(N - 1, t); ++i) {
for (int j = Math.max(0, t - (N - 1)); j <= Math.min(N - 1, t); ++j) {
if (grid[i][t - i] == -1 || grid[j][t - j] == -1) {
continue;
}
int val = grid[i][t-i];
if (i != j) {
val += grid[j][t - j];
}
for (int pi = i - 1; pi <= i; ++pi) {
for (int pj = j - 1; pj <= j; ++pj) {
if (pi >= 0 && pj >= 0) {
dp2[i][j] = Math.max(dp2[i][j], dp[pi][pj] + val);
}
}
}
}
}
dp = dp2;
}
return Math.max(0, dp[N - 1][N - 1]);
}
}
class Solution(object):
def cherryPickup(self, grid):
N = len(grid)
dp = [[float('-inf')] * N for _ in xrange(N)]
dp[0][0] = grid[0][0]
for t in xrange(1, 2 * N - 1):
dp2 = [[float('-inf')] * N for _ in xrange(N)]
for i in xrange(max(0, t - (N - 1)), min(N - 1, t) + 1):
for j in xrange(max(0, t - (N - 1)), min(N - 1, t) + 1):
if grid[i][t - i] == -1 or grid[j][t - j] == -1:
continue
val = grid[i][t - i]
if i != j:
val += grid[j][t - j]
dp2[i][j] = max(dp[pi][pj] + val
for pi in (i - 1, i) for pj in (j - 1, j)
if pi >= 0 and pj >= 0)
dp = dp2
return max(0, dp[N - 1][N - 1])
Complexity Analysis
Time Complexity:
Reason: where N is the length of
grid. We have three for-loops of size N.
Space Complexity:
Reason: the sizes of
dpanddp2.
Video Solution
References
-
LeetCode Problem: Cherry Pickup
-
Solution Link: Cherry Pickup