Binary Search
Problem Description
Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.
You must write an algorithm with runtime complexity.
Examples
Example 1:
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4
Example 2:
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1
Constraints
- All the integers in nums are unique.
numsis sorted in ascending order.
Solution for Binary Search
Approach 1: Find the Exact Value
Intuition
We start from the most basic and elementary template.
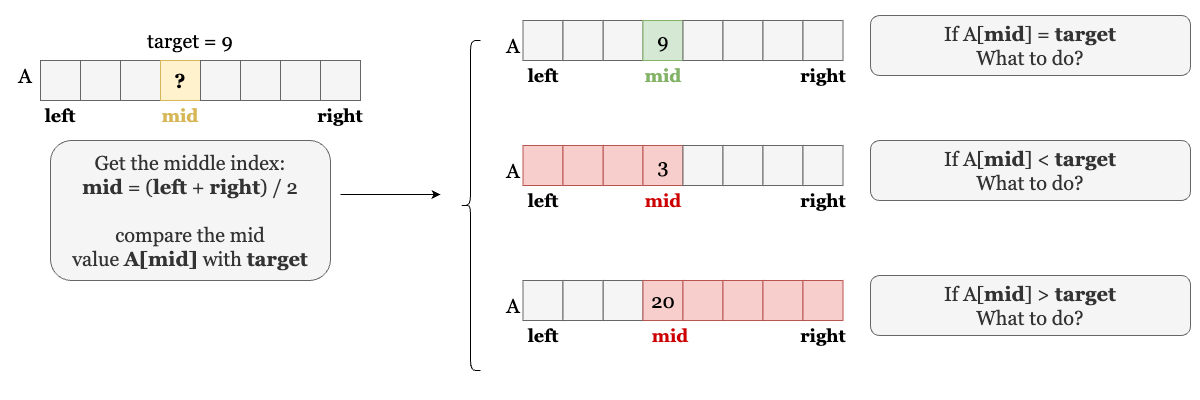
First, we define the search space using two boundary indexes, left and right, all possible indexes are within the inclusive range [left, right]. We shall continue searching over the search space as long as it is not empty. A general way is to use a while loop with the condition left <= right, so we can break out of this loop if we empty the range or trigger other conditions which we will discuss later.
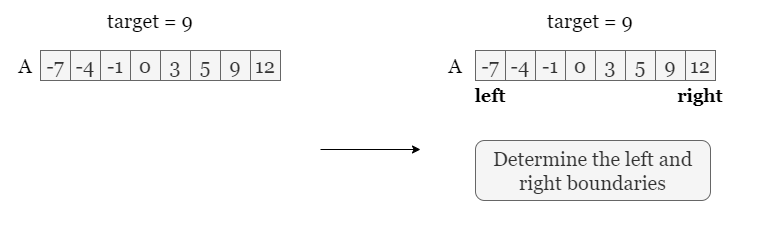
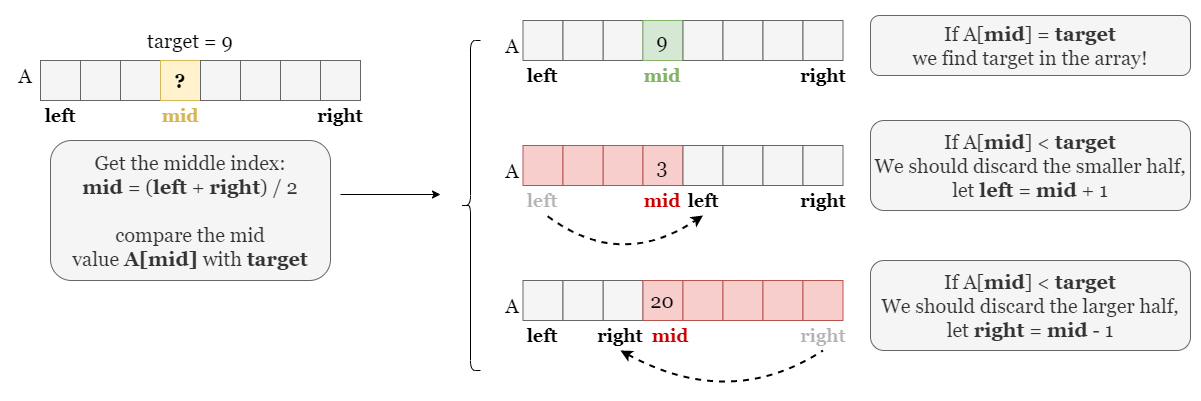
The next step is to find the 'pivot point', the middle index that divides the search space into two halves. We need to compare the value at the middle index nums[mid] with target, the purpose of this step is to cut one half that is guaranteed not to contain target.
- If
nums[mid] = target, it means we findtarget, and the job is done! We can break the loop by returning mid. - If
nums[mid] < target, combined with the array is sorted, we know that all values in the left half are smaller than target, so we can safely cut this half by lettingleft = mid + 1. - If
nums[mid] > target, it means all values in the right half are larger thantargetand can be cut safely!
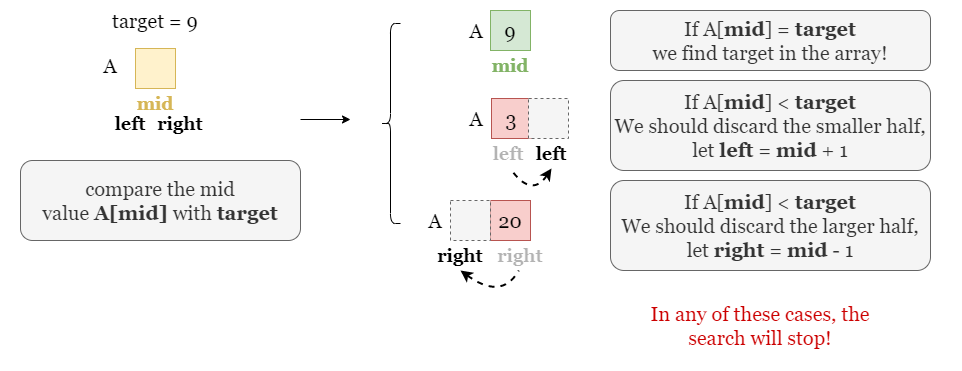
Does this loop ever stop? Yes, take the following picture as an example, suppose we are searching over an array of size 1, in this case, left, right, and mid all stand for the only index in the array. In any of the three conditions, we trigger one of the break statements and stop the loop.
Algorithm
- Initialize the boundaries of the search space as
left = 0andright = nums.size - 1. - If there are elements in the range
[left, right], we find the middle indexmid = (left + right) / 2and compare the middle valuenums[mid]withtarget:- If
nums[mid] = target, returnmid. - If
nums[mid] < target, letleft = mid + 1and repeat step 2. - If
nums[mid] > target, letright = mid - 1and repeat step 2.
- If
- We finish the loop without finding
target, return-1.
Code in Different Languages
- C++
- Java
- Python
class Solution {
public:
int search(vector<int>& nums, int target) {
// Set the left and right boundaries
int left = 0, right = int(nums.size()) - 1;
// Under this condition
while (left <= right) {
// Get the middle index and the middle value.
int mid = left + (right - left) / 2;
// Case 1, return the middle index.
if (nums[mid] == target) {
return mid;
}
// Case 2, discard the smaller half.
else if (nums[mid] < target) {
left = mid + 1;
}
// Case 3, discard the larger half.
else {
right = mid - 1;
}
}
// If we finish the search without finding target, return -1.
return -1;
}
};
class Solution {
public int search(int[] nums, int target) {
// Set the left and right boundaries
int left = 0, right = nums.length - 1;
// Under this condition
while (left <= right) {
// Get the middle index and the middle value.
int mid = left + (right - left) / 2;
// Case 1, return the middle index.
if (nums[mid] == target) {
return mid;
}
// Case 2, discard the smaller half.
else if (nums[mid] < target) {
left = mid + 1;
}
// Case 3, discard the larger half.
else {
right = mid - 1;
}
}
// If we finish the search without finding target, return -1.
return -1;
}
}
class Solution:
def search(self, nums: List[int], target: int) -> int:
# Set the left and right boundaries
left = 0
right = len(nums) - 1
# Under this condition
while left <= right:
# Get the middle index and the middle value.
mid = (left + right) // 2
# Case 1, return the middle index.
if nums[mid] == target:
return mid
# Case 2, discard the smaller half.
elif nums[mid] < target:
left = mid + 1
# Case 3, discard the larger half.
else:
right = mid - 1
# If we finish the search without finding target, return -1.
return -1
Complexity Analysis
Time Complexity:
Reason:
numsis divided into half each time. In the worst-case scenario, we need to cutnumsuntil the range has no element, and it takes logarithmic time to reach this break condition.
Space Complexity:
Reason: During the loop, we only need to record three indexes, left, right, and mid, they take constant space.
Approach 2: Find Upper bound
Intuition
Here we introduce an alternative way to implement binary search: instead of looking for target in the array nums, we look for the insert position where we can put target in without disrupting the order.

Generally, we have two inserting ways, insert into the rightmost possible position which we called finding the upper bound, and insert into the leftmost possible position which we called finding the lower bound. We will implement them in the following approaches.
Take the picture below as an example. Assume that we want to insert 9 into array A. If we look for the upper bound, we have to insert 9 to the right of all existing 9s in the array. Similarly, if we look for the lower bound, we have to insert 9 to the left of all existing 9s. (Although we don't have duplicate elements in this problem, having duplicate elements is more common in problems so we would better know this concept in advance!)
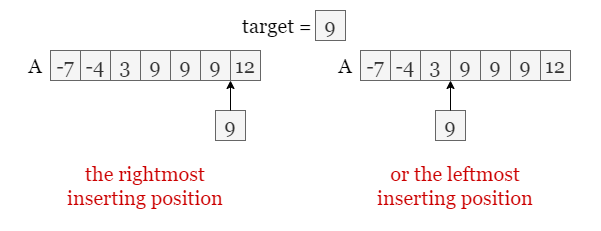
Now we start the binary search. Similar to the previous approach, we still use left and right as two boundary indexes. The question is, what is the next step after we find the middle index mid?
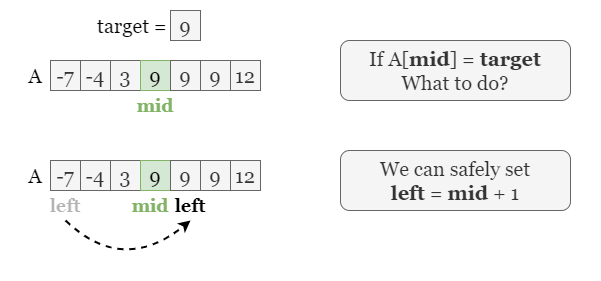
-
If
nums[mid] < target, the insert position is onmid's right, so we letleft = mid + 1to discard the left half andmid. -
If
nums[mid] = target, the insert position is onmid's right, so we letleft = mid + 1to discard the left half andmid.
- If
nums[mid] > target,midcan also be the insert position. So we letright = midto discard the right half while keepingmid.
Therefore, we merged the two conditions nums[mid] = target and nums[mid] < target and there are only two conditions in the if-else statement!
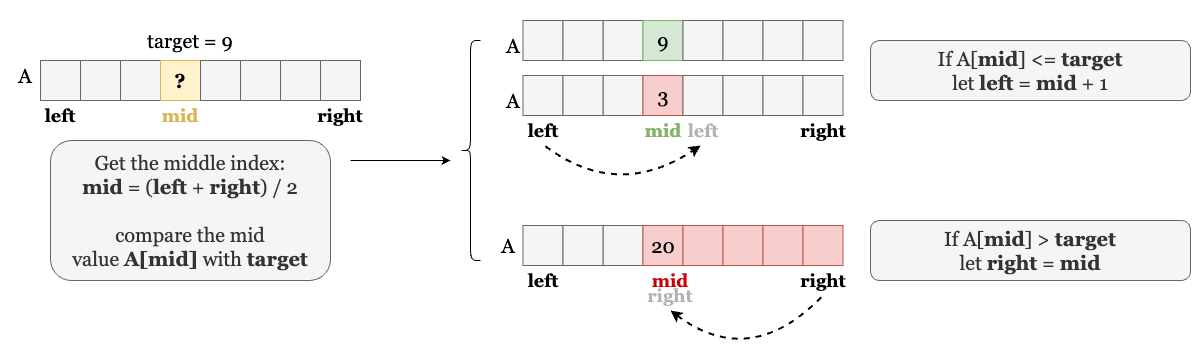
Once the loop stops, left stands for the insert position and left - 1 is the largest element that is no larger than target. We just need to check if nums[left - 1] equals target. Note this boundary condition where left = 0, which means all elements in nums are larger than target, so there is no target in nums.
Algorithm
- Initialize the boundaries of the search space as
left = 0andright = nums.size(Note that the maximum insert position can benums.size) - If there are elements in the range
[left, right], we find the middle indexmid = (left + right) / 2and compare the middle valuenums[mid]with target:- If
nums[mid] <= target, letleft = mid + 1and repeat step 2. - If
nums[mid] > target, letright = midand repeat step 2.
- If
- We finish the loop and
leftstands for the insert position:- If
left > 0andnums[left - 1] = target, returnleft - 1. - Otherwise, return
-1.
- If
Code in Different Languages
- C++
- Java
- Python
class Solution {
public:
int search(vector<int>& nums, int target) {
// Set the left and right boundaries
int left = 0, right = int(nums.size());
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] <= target) {
left = mid + 1;
} else {
right = mid;
}
}
if (left > 0 and nums[left - 1] == target) {
return left - 1;
} else {
return -1;
}
}
};
class Solution {
public int search(int[] nums, int target) {
// Set the left and right boundaries
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] <= target) {
left = mid + 1;
} else {
right = mid;
}
}
if (left > 0 && nums[left - 1] == target) {
return left - 1;
} else {
return -1;
}
}
}
class Solution:
def search(self, nums: List[int], target: int) -> int:
# Set the left and right boundaries
left = 0
right = len(nums)
while left < right:
mid = (left + right) // 2
if nums[mid] <= target:
left = mid + 1
else:
right = mid
if left > 0 and nums[left - 1] == target:
return left - 1
else:
return -1
Complexity Analysis
Time Complexity:
Reason:
numsis divided into half each time. In the worst-case scenario, we need to cutnumsuntil the range has no element, it takes logarithmic time to reach this break condition.
Space Complexity:
Reason: During the loop, we only need to record three indexes,
left,right, andmid, they take constant space.
References
-
LeetCode Problem: Binary Search
-
Solution Link: Binary Search