Unique Paths

Problem Description

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Examples

Example 1:

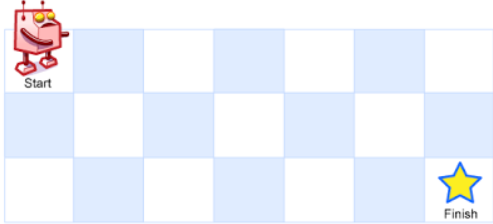
Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

Constraints

• 1 <= m, n <= 100

Solution for Unique Paths

Approach

Brute Force

• The brute force approach uses recursion to explore all possible paths from the top-left to the bottom-right corner of the grid. At each cell, the robot has two choices: move right or move down.

Recursive function:

int uniquePathsBruteForce(int m, int n) {
    if (m == 1 || n == 1) {
        return 1;
    }
    return uniquePathsBruteForce(m - 1, n) + uniquePathsBruteForce(m, n - 1);
}

Complexity:

• Time Complexity: O(2^(m+n)) - Each recursive call generates two more recursive calls, leading to an exponential number of calls.
• Space Complexity: O(m+n) - The recursion stack can go as deep as the sum of m and n.

Corner Cases:

• If m or n is 1, there's only one path straight to the destination.
• The function assumes valid input where m and n are positive integers.

Optimized Approach

• The optimized approach uses dynamic programming to avoid redundant calculations. We create a 2D array dp where dp[i][j] represents the number of unique paths to reach cell (i, j).

Dynamic Programming Solution:

int uniquePaths(int m, int n) {
    vector<vector<int>> dp(m, vector<int>(n, 1));
    
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    
    return dp[m-1][n-1];
}

Complexity:

• Time Complexity: O(m*n) because We fill in each cell of the m x n matrix exactly once.
• Space Complexity: O(m*n) We use a 2D array to store the number of paths for each cell.

Further Optimization We can further optimize the space complexity to O(n) by using a single array to keep track of the current row's path counts.

int uniquePaths(int m, int n) {
    vector<int> dp(n, 1);
    
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[j] += dp[j-1];
        }
    }
    
    return dp[n-1];
}

Complexity of Optimized Approach:

• Time Complexity: O(m*n) - Still filling in each cell exactly once.
• Space Complexity: O(n) - Using a single array of size n.

Corner Cases:

• If either m or n is 1, the function should return 1 since there's only one path straight to the destination.
• TThe function handles cases where m or n is very large efficiently within the constraints

Solution

Implementation

Live Editor

function Solution(a,b) {
  var uniquePaths = function(m, n) {
    if (m === 0 || n === 0) return 0;

    let dp = new Array(n).fill(1);

    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            dp[j] += dp[j - 1];
        }
    }

    return dp[n - 1];
  };

  const m = 3;
  const n = 7;
  const output = uniquePaths(m, n);
  return (
    <div>
      <p>
        <b>Input: </b>
        {m,' ',n}
      </p>
      <p>
        <b>Output:</b> {output.toString()}
      </p>
    </div>
  );
}

Result

Loading...

Complexity Analysis

• Time Complexity: $O(m*n)$
• Space Complexity: $O(n)$

Code in Different Languages

JavaScript

Written by @vansh-codes

     var uniquePaths = function(m, n) {
         if (m === 0 || n === 0) return 0;

         let dp = new Array(n).fill(1);

         for (let i = 1; i < m; i++) {
             for (let j = 1; j < n; j++) {
                 dp[j] += dp[j - 1];
             }
         }
         return dp[n - 1];
     };

TypeScript

Written by @vansh-codes

     function uniquePaths(m: number, n: number): number {
         if (m === 0 || n === 0) return 0;

         let dp: number[] = new Array(n).fill(1);

         for (let i = 1; i < m; i++) {
             for (let j = 1; j < n; j++) {
                 dp[j] += dp[j - 1];
             }
         }

         return dp[n - 1];
     };

Python

Written by @vansh-codes

 class Solution(object):
     def uniquePaths(self, m, n):
         if m == 0 or n == 0:
             return 0
         
         dp = [1] * n
         
         for i in range(1, m):
             for j in range(1, n):
                 dp[j] += dp[j - 1]
         
         return dp[-1]

Java

Written by @vansh-codes

 class Solution {
     public int uniquePaths(int m, int n) {
         if (m == 0 || n == 0) return 0;

         int[] dp = new int[n];
         Arrays.fill(dp, 1);

         for (int i = 1; i < m; i++) {
             for (int j = 1; j < n; j++) {
                 dp[j] += dp[j - 1];
             }
         }

         return dp[n - 1];
     }
 }

C++

Written by @vansh-codes

class Solution {
 public:
     int uniquePaths(int m, int n) {
         if (m == 0 || n == 0) return 0;

         vector<int> dp(n, 1);

         for (int i = 1; i < m; i++) {
             for (int j = 1; j < n; j++) {
                 dp[j] += dp[j - 1];
             }
         }

         return dp[n - 1];
     }
 };

References

• LeetCode Problem: Unique Paths

• Solution Link: LeetCode Solution