Minimum Time to Collect All Apples in a Tree
Problem Description
Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.
The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.
Examples
Example 1:
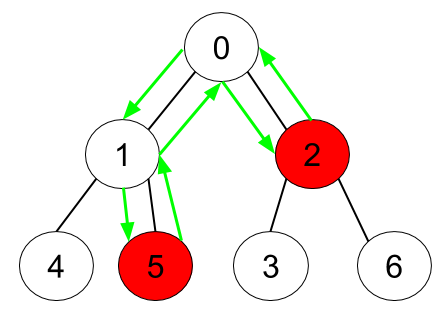
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
Example 2:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
Constraints
1 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai < bi <= n - 1hasApple.length == n
Solution for Diagonal Traverse II Problem
Approach
The problem can be solved using Depth-First Search (DFS). The main idea is to traverse the tree, and whenever an apple is found in a subtree, add the cost of traveling to and from that subtree to the total time. If a subtree does not contain any apples, it can be skipped.
Steps to Solve
-
Construct the Adjacency List:
- Create an adjacency list to represent the tree from the given edges.
-
Depth-First Search (DFS):
- Perform a DFS starting from the root node (0).
- For each node, recursively calculate the total travel cost for its children.
- If a child node has an apple, include the travel cost of going to the child and returning to the current node (cost of 2).
- Mark the current node as having an apple if any of its children have apples, ensuring that the parent nodes consider the travel costs for collecting apples from their subtrees.
-
Return the Result:
- The DFS function returns the total travel cost required to collect all apples and return to the root node.
- Solution
Implementation
function Solution(arr) { function dfs(adj, hasApple, node, parent) { let distance = 0; for (let i of adj[node]) { if (i !== parent) { let temp = dfs(adj, hasApple, i, node); if (hasApple[i]) { distance += (2 + temp); hasApple[node] = true; } } } return distance; } function minTime(n, edges, hasApple) { let adj = Array.from({ length: n }, () => []); for (let [u, v] of edges) { adj[u].push(v); adj[v].push(u); } return dfs(adj, hasApple, 0, 0); } const input = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false] const output = minTime(input , edges , hasApple) return ( <div> <p> <b>Input: </b> {JSON.stringify(input)} <b>edges: </b> {JSON.stringify(edges)} <b>hasApple: </b> {JSON.stringify(hasApple)} </p> <p> <b>Output:</b> {output.toString()} </p> </div> ); }
Complexity Analysis
- Time Complexity:
- Space Complexity:
Code in Different Languages
- JavaScript
- TypeScript
- Python
- Java
- C++
class Solution {
dfs(adj, hasApple, node, parent) {
let distance = 0;
for (let i of adj[node]) {
if (i !== parent) {
let temp = this.dfs(adj, hasApple, i, node);
if (hasApple[i]) {
distance += (2 + temp);
hasApple[node] = true;
}
}
}
return distance;
}
minTime(n, edges, hasApple) {
let adj = Array.from({ length: n }, () => []);
for (let [u, v] of edges) {
adj[u].push(v);
adj[v].push(u);
}
return this.dfs(adj, hasApple, 0, 0);
}
}
class Solution {
private dfs(adj: number[][], hasApple: boolean[], node: number, parent: number): number {
let distance = 0;
for (let i of adj[node]) {
if (i !== parent) {
let temp = this.dfs(adj, hasApple, i, node);
if (hasApple[i]) {
distance += (2 + temp);
hasApple[node] = true;
}
}
}
return distance;
}
minTime(n: number, edges: number[][], hasApple: boolean[]): number {
let adj: number[][] = Array.from({ length: n }, () => []);
for (let [u, v] of edges) {
adj[u].push(v);
adj[v].push(u);
}
return this.dfs(adj, hasApple, 0, 0);
}
}
class Solution:
def dfs(self, adj, hasApple, node, parent):
distance = 0
for i in adj[node]:
if i != parent:
temp = self.dfs(adj, hasApple, i, node)
if hasApple[i]:
distance += 2 + temp
hasApple[node] = True
return distance
def minTime(self, n, edges, hasApple):
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
return self.dfs(adj, hasApple, 0, 0)
import java.util.*;
class Solution {
public int dfs(List<Integer>[] adj, List<Boolean> hasApple, int node, int parent) {
int distance = 0;
for (int i : adj[node]) {
if (i != parent) {
int temp = dfs(adj, hasApple, i, node);
if (hasApple.get(i)) {
distance += 2 + temp;
hasApple.set(node, true);
}
}
}
return distance;
}
public int minTime(int n, List<List<Integer>> edges, List<Boolean> hasApple) {
List<Integer>[] adj = new ArrayList[n];
for (int i = 0; i < n; i++) {
adj[i] = new ArrayList<>();
}
for (List<Integer> edge : edges) {
int u = edge.get(0);
int v = edge.get(1);
adj[u].add(v);
adj[v].add(u);
}
return dfs(adj, hasApple, 0, 0);
}
}
class Solution {
public:
int dfs(vector<int> adj[], vector<bool> &hasApple, int node, int parent) {
int distance = 0;
for(auto i:adj[node]) {
if(i!=parent) {
int temp=dfs(adj, hasApple, i, node);
if(hasApple[i]) {
distance+=(2+temp);
hasApple[node]=true;
}
}
}
return distance;
}
int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
vector<int> adj[n];
for(int i=0;i<edges.size();i++) {
adj[edges[i][0]].push_back(edges[i][1]);
adj[edges[i][1]].push_back(edges[i][0]);
}
return dfs(adj, hasApple, 0, 0);
}
};
References
-
LeetCode Problem: Minimum Time to Collect All Apples in a Tree
-
Solution Link: LeetCode Solution