Vertical Order Traversal of a Binary Tree
Problem Description
Given the root of a binary tree, calculate the vertical order traversal of the binary tree.
For each node at position (row, col), its left and right children will be at positions (row + 1, col - 1) and (row + 1, col + 1) respectively. The root of the tree is at (0, 0).
The vertical order traversal of a binary tree is a list of top-to-bottom orderings for each column index starting from the leftmost column and ending on the rightmost column. There may be multiple nodes in the same row and same column. In such a case, sort these nodes by their values.
Return the vertical order traversal of the binary tree.
Examples
Example 1:
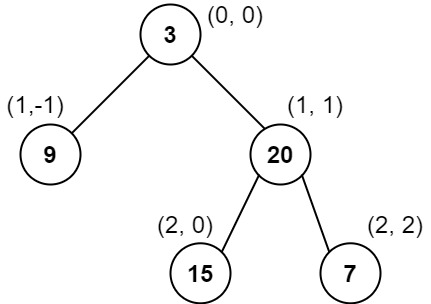
Input: root = [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation:
Column -1: Only node 9 is in this column.
Column 0: Nodes 3 and 15 are in this column in that order from top to bottom.
Column 1: Only node 20 is in this column.
Column 2: Only node 7 is in this column.
Example 2:
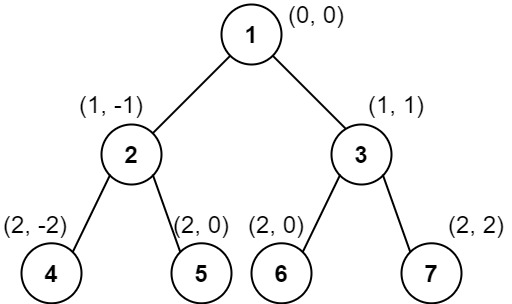
Input: root = [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation:
Column -2: Only node 4 is in this column.
Column -1: Only node 2 is in this column.
Column 0: Nodes 1, 5, and 6 are in this column.
1 is at the top, so it comes first.
5 and 6 are at the same position (2, 0), so we order them by their value, 5 before 6.
Column 1: Only node 3 is in this column.
Column 2: Only node 7 is in this column.
Example 3:
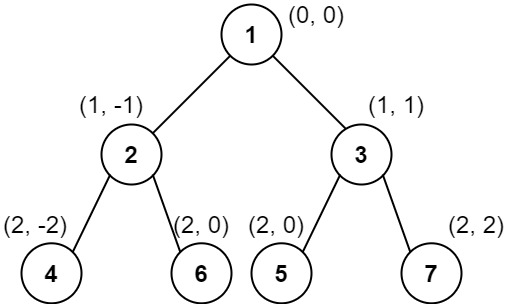
Input: root = [1,2,3,4,6,5,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation:
This case is the exact same as example 2, but with nodes 5 and 6 swapped.
Note that the solution remains the same since 5 and 6 are in the same location and should be ordered by their values.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 1000
Solution for Vertical Order Traversal of a Binary Tree
Approach:
- The approach involves performing a breadth-first search (BFS) traversal of the tree while keeping track of the positions
(row, col)of each node. - We use a dictionary to map column indices to lists of nodes and their respective rows.
- Finally, we sort these lists by row and node value and return the result in column order.
Steps:
- Perform a BFS traversal of the tree.
- For each node, track its
(row, col)position. - Use a dictionary to store nodes by their column index.
- For nodes in the same column and row, sort them by their values. = Return the vertical order traversal from the leftmost to the rightmost column.
Explanation
- BFS Traversal: We use a queue to perform a level-order traversal while tracking each node's row and column.
- Dictionary Storage: Nodes are stored in a dictionary where keys are column indices, and values are lists of tuples containing
(row, value)of the nodes. - Sorting: For each column, nodes are sorted first by row and then by value.
- Result Compilation: The final result is compiled by traversing columns in sorted order and extracting node values.
Corner Cases:
- A tree with only one node.
- A skewed tree (all nodes in a single line).
Code in Different Languages
Code(C++):
from collections import defaultdict, deque
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def verticalTraversal(root: TreeNode):
nodes = defaultdict(list)
queue = deque([(root, 0, 0)])
while queue:
node, row, col = queue.popleft()
if node:
nodes[col].append((row, node.val))
queue.append((node.left, row + 1, col - 1))
queue.append((node.right, row + 1, col + 1))
result = []
for col in sorted(nodes):
result.append([val for row, val in sorted(nodes[col])])
return result
Code(Java):
java
Copy code
import java.util.*;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int val) { this.val = val; }
}
class Solution {
public List<List<Integer>> verticalTraversal(TreeNode root) {
Map<Integer, List<int[]>> nodes = new HashMap<>();
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{root.val, 0, 0, System.identityHashCode(root)});
while (!queue.isEmpty()) {
int[] nodeData = queue.poll();
int val = nodeData[0], row = nodeData[1], col = nodeData[2], hash = nodeData[3];
TreeNode node = getNodeByHash(hash, root);
if (!nodes.containsKey(col)) nodes.put(col, new ArrayList<>());
nodes.get(col).add(new int[]{row, val});
if (node.left != null)
queue.offer(new int[]{node.left.val, row + 1, col - 1, System.identityHashCode(node.left)});
if (node.right != null)
queue.offer(new int[]{node.right.val, row + 1, col + 1, System.identityHashCode(node.right)});
}
List<List<Integer>> result = new ArrayList<>();
for (int col : new TreeSet<>(nodes.keySet())) {
List<int[]> nodeList = nodes.get(col);
nodeList.sort((a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
List<Integer> colVals = new ArrayList<>();
for (int[] node : nodeList) {
colVals.add(node[1]);
}
result.add(colVals);
}
return result;
}
private TreeNode getNodeByHash(int hash, TreeNode root) {
if (System.identityHashCode(root) == hash) return root;
TreeNode node = null;
if (root.left != null) node = getNodeByHash(hash, root.left);
if (node == null && root.right != null) node = getNodeByHash(hash, root.right);
return node;
}
}
Code(C++)
cpp
Copy code
#include <map>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
vector<vector<int>> verticalTraversal(TreeNode* root) {
map<int, vector<pair<int, int>>> nodes;
queue<pair<TreeNode*, pair<int, int>>> q;
q.push({root, {0, 0}});
while (!q.empty()) {
auto p = q.front();
q.pop();
TreeNode* node = p.first;
int row = p.second.first, col = p.second.second;
nodes[col].push_back({row, node->val});
if (node->left) q.push({node->left, {row + 1, col - 1}});
if (node->right) q.push({node->right, {row + 1, col + 1}});
}
vector<vector<int>> result;
for (auto& col : nodes) {
sort(col.second.begin(), col.second.end());
vector<int> colVals;
for (auto& node : col.second) {
colVals.push_back(node.second);
}
result.push_back(colVals);
}
return result;
}
};
Complexity:
Time Complexity: where N is the number of nodes in the tree. Sorting nodes for each column contributes to the log factor.
Space Complexity: due to the storage of node positions and the queue for BFS traversal.