Binary Tree Cameras
Problem Description
You are given the root of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return the minimum number of cameras needed to monitor all nodes of the tree.
Examples
Example 1:
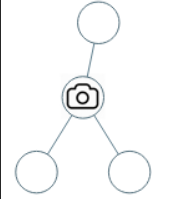
Input: root = [0,0,null,0,0]
Output: 1
Explanation: One camera is enough to monitor all nodes if placed as shown.
Example 2:
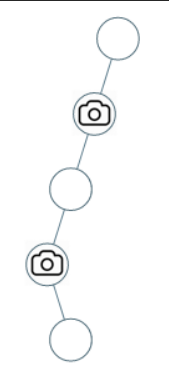
Input: root = [0,0,null,0,null,0,null,null,0]
Output: 2
Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
Constraints
- The number of nodes in the tree is in the range
[1, 1000]. Node.val == 0
Solution for Binary Tree Cameras
Approach 1
Brute Force
The brute force approach involves exploring all possible ways to place cameras and selecting the minimum configuration. This is impractical due to the exponential number of configurations.
Steps::
- For each node, consider placing a camera at that node.
- Recursively determine the number of cameras needed for the left and right subtrees.
- Calculate the total number of cameras for each configuration and choose the minimum.
Complexity:
- Time Complexity:
O(2^n)wherenis the number of nodes in the tree. This is because each node has two possibilities: placing a camera or not. - Space Complexity:
O(n)due to the recursion stack.
Corner Cases:
- An empty tree (should return 0).
- A single node tree (should return 1).
- A skewed tree where all nodes are in a single line (worst-case scenario for brute force).
Approach 2
Optimized Approach
The optimized approach uses dynamic programming with a Depth-First Search (DFS) traversal. The idea is to use three states for each node:
- State 0: The node has no camera and is not monitored.
- State 1: The node is monitored but does not have a camera.
- State 2: The node has a camera.
We then use these states to determine the minimum number of cameras needed.
Steps:
- Define a recursive function
dfs(node)that returns a tuple of three values representing the minimum cameras needed for states 0, 1, and 2. - For each node, compute:
- State 0: The sum of the minimum cameras needed for state 1 of the left and right children.
- State 1: The minimum of state 2 (placing a camera) for either left or right child plus the minimum of states 0 or 1 for the other child.
- State 2: 1 (camera at this node) plus the minimum of states 0, 1, or 2 for both left and right children.
- The result for the root is the minimum of state 1 and state 2.
Implementation:
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def minCameraCover(root: TreeNode) -> int:
def dfs(node):
if not node:
return (0, 0, float('inf'))
L = dfs(node.left)
R = dfs(node.right)
d0 = L[1] + R[1]
d1 = min(L[2] + min(R[1], R[2]), R[2] + min(L[1], L[2]))
d2 = 1 + min(L) + min(R)
return (d0, d1, d2)
res = dfs(root)
return min(res[1], res[2])
Explanation:
- dfs(node): Returns a tuple (d0, d1, d2) for the given node.
d0: Minimum cameras needed if the node is not monitored.d1: Minimum cameras needed if the node is monitored but has no camera.d2: Minimum cameras needed if the node has a camera.
- Res: For the root node, we return the minimum of
d1andd2, ensuring all nodes are monitored.
Complexity:
- Time Complexity:
O(n)wherenis the number of nodes. Each node is visited once - Space Complexity:
O(h)wherehis the height of the tree due to the recursion stack.
Corner Cases:
- An empty tree (should return 0).
- A single node tree (should return 1).
- A skewed tree where all nodes are in a single line.
Code in Different Languages
- JavaScript
- TypeScript
- Python
- Java
- C++
var minCameraCover = function(root) {
const NOT_NEEDED = 0;
const HAS_CAMERA = 1;
const NEEDS_CAMERA = 2;
let cameras = 0;
function dfs(node) {
if (!node) return NOT_NEEDED;
const left = dfs(node.left);
const right = dfs(node.right);
if (left === NEEDS_CAMERA || right === NEEDS_CAMERA) {
cameras++;
return HAS_CAMERA;
}
if (left === HAS_CAMERA || right === HAS_CAMERA) {
return NOT_NEEDED;
}
return NEEDS_CAMERA;
}
return dfs(root) === NEEDS_CAMERA ? cameras + 1 : cameras;
};
function minCameraCover(root: TreeNode | null): number {
const NOT_NEEDED = 0;
const HAS_CAMERA = 1;
const NEEDS_CAMERA = 2;
let cameras = 0;
function dfs(node: TreeNode | null): number {
if (!node) return NOT_NEEDED;
const left = dfs(node.left);
const right = dfs(node.right);
if (left === NEEDS_CAMERA || right === NEEDS_CAMERA) {
cameras++;
return HAS_CAMERA;
}
if (left === HAS_CAMERA || right === HAS_CAMERA) {
return NOT_NEEDED;
}
return NEEDS_CAMERA;
}
return dfs(root) === NEEDS_CAMERA ? cameras + 1 : cameras;
};
class Solution:
def minCameraCover(self, root: Optional[TreeNode]) -> int:
NOT_NEEDED = 0
HAS_CAMERA = 1
NEEDS_CAMERA = 2
cameras = 0
def dfs(node):
nonlocal cameras
if not node:
return NOT_NEEDED
left = dfs(node.left)
right = dfs(node.right)
if left == NEEDS_CAMERA or right == NEEDS_CAMERA:
cameras += 1
return HAS_CAMERA
if left == HAS_CAMERA or right == HAS_CAMERA:
return NOT_NEEDED
return NEEDS_CAMERA
return cameras + 1 if dfs(root) == NEEDS_CAMERA else cameras
class Solution {
private static final int NOT_NEEDED = 0;
private static final int HAS_CAMERA = 1;
private static final int NEEDS_CAMERA = 2;
private int cameras = 0;
public int minCameraCover(TreeNode root) {
return (dfs(root) == NEEDS_CAMERA ? 1 : 0) + cameras;
}
private int dfs(TreeNode node) {
if (node == null) return NOT_NEEDED;
int left = dfs(node.left);
int right = dfs(node.right);
if (left == NEEDS_CAMERA || right == NEEDS_CAMERA) {
cameras++;
return HAS_CAMERA;
}
if (left == HAS_CAMERA || right == HAS_CAMERA) {
return NOT_NEEDED;
}
return NEEDS_CAMERA;
}
}
class Solution {
static const int NOT_NEEDED = 0;
static const int HAS_CAMERA = 1;
static const int NEEDS_CAMERA = 2;
int cameras = 0;
int dfs(TreeNode* node) {
if (!node) return NOT_NEEDED;
int left = dfs(node->left);
int right = dfs(node->right);
if (left == NEEDS_CAMERA || right == NEEDS_CAMERA) {
cameras++;
return HAS_CAMERA;
}
if (left == HAS_CAMERA || right == HAS_CAMERA) {
return NOT_NEEDED;
}
return NEEDS_CAMERA;
}
public:
int minCameraCover(TreeNode* root) {
return (dfs(root) == NEEDS_CAMERA ? 1 : 0) + cameras;
}
};
References
-
LeetCode Problem: Binary Tree Cameras
-
Solution Link: LeetCode Solution