Path Sum III
Problem Description
Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum. The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).
Examples
Example 1:
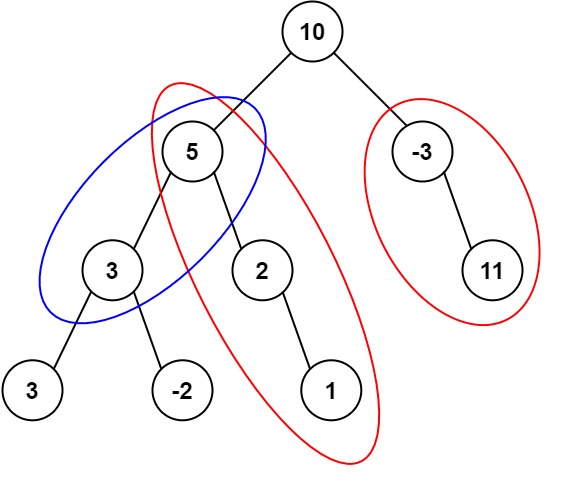
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.
Example 2:
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: 3
Constraints
- The number of nodes in the tree is in the range [0, 1000].
-10^9 <= Node.val <= 10^9-1000 <= targetSum <= 1000
Solution for Path Sum III
Approach
Tree Traversal:
- The main idea is to traverse the binary tree. This is achieved using a recursive function solve that explores all nodes starting from the root.
- The traversal is done using Depth First Search (DFS), ensuring all possible paths from the root to the leaves are explored.
Path Tracking:
- During traversal, we maintain a path vector that keeps track of the nodes' values along the current path from the root to the current node.
- As we visit each node, its value is added to the path.
Path Sum Calculation:
- After adding a node’s value to the path, we check all sub-paths ending at the current node to see if any of them sum to the targetSum.
- We iterate backwards through the path vector, accumulating the sum and checking if it matches the targetSum.
- If a sub-path's sum matches targetSum, we increment the count.
Backtracking:
- After checking the sub-paths for the current node, we backtrack by removing the current node's value from the path.
- This ensures that the path vector only contains nodes along the current path in the DFS traversal.
- Solution
Implementation
function pathSum3() { function TreeNode(val = 0, left = null, right = null) { this.val = val; this.left = left; this.right = right; } function constructTreeFromArray(array) { if (!array.length) return null; let root = new TreeNode(array[0]); let queue = [root]; let i = 1; while (i < array.length) { let currentNode = queue.shift(); if (array[i] !== null) { currentNode.left = new TreeNode(array[i]); queue.push(currentNode.left); } i++; if (i < array.length && array[i] !== null) { currentNode.right = new TreeNode(array[i]); queue.push(currentNode.right); } i++; } return root; } function pathSum(root, targetSum) { // Map to keep the cumulative sum and its frequency. const prefixSumCount = new Map(); // Helper function to perform DFS on the tree and calculate paths. function dfs(node, currentSum) { if (!node) { return 0; } // Update the current sum by adding the node's value. currentSum += node.val; // Get the number of times we have seen the currentSum - targetSum. let pathCount = prefixSumCount.get(currentSum - targetSum) || 0; // Update the count of the current sum in the map. prefixSumCount.set(currentSum, (prefixSumCount.get(currentSum) || 0) + 1); // Explore left and right subtrees. pathCount += dfs(node.left, currentSum); pathCount += dfs(node.right, currentSum); // After returning from the recursion, decrement the frequency of the current sum. prefixSumCount.set(currentSum, (prefixSumCount.get(currentSum) || 0) - 1); // Return the total count of paths found. return pathCount; } // Initialize the map with base case before the recursion. prefixSumCount.set(0, 1); // Start DFS from the root node with an initial sum of 0. return dfs(root, 0); } const array =[10, 5, -3, 3, 2, null, 11, 3, -2, null, 1]; const root = constructTreeFromArray(array) const input = root const targetSum = 8; const output = pathSum(input ,targetSum) return ( <div> <p> <b>Input: </b>{JSON.stringify(array)} </p> <p> <b>Output:</b> {output.toString()} </p> </div> ); }
Code in Different Languages
- JavaScript
- TypeScript
- Python
- Java
- C++
function TreeNode(val, left = null, right = null) {
return {
val: val,
left: left,
right: right
};
}
function pathSum3(root, targetSum) {
function solve(node, targetSum, count, path) {
if (!node) {
return;
}
path.push(node.val);
pathSumHelper(node, targetSum, count, path);
solve(node.left, targetSum, count, path.slice());
solve(node.right, targetSum, count, path.slice());
}
function pathSumHelper(node, targetSum, count, path) {
let sum = 0;
for (let i = path.length - 1; i >= 0; i--) {
sum += path[i];
if (sum === targetSum) {
count[0]++;
}
}
}
const path = [];
const count = [0];
solve(root, targetSum, count, path);
return count[0];
}
interface TreeNode {
val: number;
left?: TreeNode | null;
right?: TreeNode | null;
}
function solve(root: TreeNode | null, targetSum: number, count: number[], path: number[]): void {
if (!root) {
return;
}
path.push(root.val);
pathSumHelper(root, targetSum, count, path);
solve(root.left, targetSum, count, path.slice());
solve(root.right, targetSum, count, path.slice());
}
function pathSumHelper(node: TreeNode, targetSum: number, count: number[], path: number[]): void {
let sum = 0;
for (let i = path.length - 1; i >= 0; i--) {
sum += path[i];
if (sum === targetSum) {
count[0]++;
}
}
}
function pathSum(root: TreeNode | null, targetSum: number): number {
const path: number[] = [];
const count: number[] = [0];
solve(root, targetSum, count, path);
return count[0];
}
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def solve(self, root, targetSum, count, path):
if not root:
return
path.append(root.val)
self.path_sum_helper(root, targetSum, count, path)
self.solve(root.left, targetSum, count, path[:])
self.solve(root.right, targetSum, count, path[:])
def path_sum_helper(self, node, targetSum, count, path):
_sum = 0
for val in reversed(path):
_sum += val
if _sum == targetSum:
count[0] += 1
def pathSum(self, root, targetSum):
path = []
count = [0]
self.solve(root, targetSum, count, path)
return count[0]
import java.util.ArrayList;
import java.util.List;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public class Solution {
public void solve(TreeNode root, int targetSum, int[] count, List<Integer> path) {
if (root == null) {
return;
}
path.add(root.val);
pathSumHelper(root, targetSum, count, path);
solve(root.left, targetSum, count, new ArrayList<>(path));
solve(root.right, targetSum, count, new ArrayList<>(path));
}
public void pathSumHelper(TreeNode node, int targetSum, int[] count, List<Integer> path) {
int sum = 0;
for (int i = path.size() - 1; i >= 0; i--) {
sum += path.get(i);
if (sum == targetSum) {
count[0]++;
}
}
}
public int pathSum(TreeNode root, int targetSum) {
List<Integer> path = new ArrayList<>();
int[] count = new int[1];
solve(root, targetSum, count, path);
return count[0];
}
}
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
void solve(TreeNode * root,int targetSum,int &count,vector<int>path)
{
if(root==NULL)
{
return;
}
path.push_back(root->val);
solve(root->left,targetSum,count,path);
solve(root->right,targetSum,count,path);
int size=path.size();
long long sum=0;
for(int i=size-1;i>=0;i--)
{
sum+=path[i];
if(sum==targetSum)
count++;
}
path.pop_back();
}
int pathSum(TreeNode* root, int targetSum) {
vector<int>path;
int count=0;
solve(root,targetSum,count,path);
return count;
}
Complexity Analysis
Time Complexity:
-
Tree Traversal (DFS): We visit each node exactly once during the Depth First Search (DFS). For a binary tree with n nodes, this traversal takes time.
-
Sub-Path Sum Calculation: At each node, we check all sub-paths ending at that node. The maximum number of sub-paths to check is equal to the depth of the tree, which in the worst case (a skewed tree) is .Thus, for each node, the sum checking operation takes in the worst case. Combining these two parts, the total time complexity is ×= in the worst case.
Space Complexity:
References
-
LeetCode Problem: Path Sum III
-
Solution Link: LeetCode Solution