Add Two Numbers II
Problem Description
You are given two non-empty linked lists representing two non-negative integers. The most significant digit comes first and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Examples
Example 1:
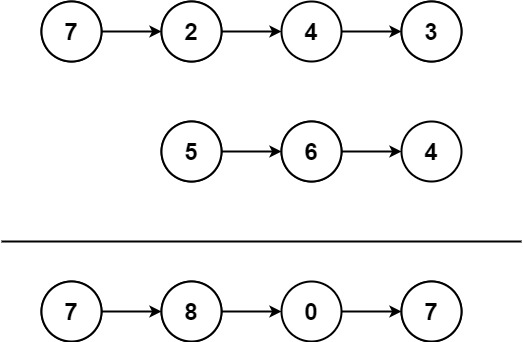
Input: l1 = [7,2,4,3], l2 = [5,6,4]
Output: [7,8,0,7]
Example 2:
Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [8,0,7]
Constraints
- The number of nodes in each linked list is in the range
[1, 100]. 0 <= Node.val <= 9- It is guaranteed that the list represents a number that does not have leading zeros.
Solution for Add Two Numbers II
Approach 1: Reverse Given Linked Lists
Intuition
We are told that the most significant digit comes first, and that each of their nodes includes a single digit. To do a basic addition of two numbers using a sum of two digits and a carry, we must start with the least significant digits (the lowest place) and work our way up to the most significant digits.
To get the order of digits from the least significant digits to the the most significant digits, we can reverse the given lists so the least significant digits come first.
We can then iterate over the reversed lists to perform the addition of digits at corresponding places similar to the first approach.
Let's understand how to reverse a linked list.
To reverse a linked list, we need three pointers. The first pointer head points to the current node under consideration, temp points to the next node, and prev points to the previous node. This is because while traversing the list, we change the current node's (head) next pointer to point to its previous element (prev). Since a node does not have reference to its previous node, we must store its previous element beforehand. We also need another pointer to store the next node (temp) before changing the reference so we don't lose it after changing head.next.
We start with initializing prev to null. We then loop until head is null, i.e., until we iterate over all the elements. We store head.next in temp to store the next node we will go to. After storing the next node, we reverse next of head to the previous element, i.e., head.next = prev. We then move prev to head as this becomes the previous node for the next node and also move head to temp as this becomes the new node under consideration.
Algorithm
- Create two linked lists
r1andr2to store the reverse of the linked listsl1andl2respectively. - Create two integers
totalSumandcarryto store the sum and carry of current digits. - Create a new
ListNode,ansthat will store the sum of current digits. - We will add the two numbers using the reverse list by adding the digits one by one. We continue until we cover all the nodes in
r1andr2:- If
r1is not null, we addr1.valtototalSum. - If
r2is not null, we addr2.valtototalSum. - Set `ans.val = totalSum % 10.
- Store the
carryastotalSum / 10. - Create a new
ListNode,newNodethat will havevalascarry. SetnextofnewNodetoans. Updateans = newNodeto use the same variableansfor the next iteration. - Update
totalSum = carry.
- If
- If
carry == 0, it means the newNode that we created in the final iteration of while loop hasval = 0. Because we performans = newNodeat the end of each while loop iteration while loop, to avoid returning a linked list with a head of0(leading zero), we return the next element, i.e., we returnans.next. Otherwise, ifcarryis not equal to0, the value ofansis non-zero. Hence, we just returnans.
Code in Different Languages
- C++
- Java
- Python
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr;
ListNode* temp;
while (head) {
// Keep the next node.
temp = head->next;
// reverse the link
head->next = prev;
// Update the previous node and the current node.
prev = head;
head = temp;
}
return prev;
}
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* r1 = reverseList(l1);
ListNode* r2 = reverseList(l2);
int totalSum = 0;
int carry = 0;
ListNode* ans = new ListNode();
while (r1 || r2) {
if (r1) {
totalSum += r1->val;
r1 = r1->next;
}
if (r2) {
totalSum += r2->val;
r2 = r2->next;
}
ans->val = totalSum % 10;
carry = totalSum / 10;
ListNode* head = new ListNode(carry);
head->next = ans;
ans = head;
totalSum = carry;
}
return carry == 0 ? ans->next : ans;
}
};
public class Solution {
public ListNode reverseList(ListNode head) {
ListNode prev = null, temp;
while (head != null) {
// Keep the next node
temp = head.next;
// Reverse the link
head.next = prev;
// Update the previous node and the current node.
prev = head;
head = temp;
}
return prev;
}
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode r1 = reverseList(l1);
ListNode r2 = reverseList(l2);
int totalSum = 0, carry = 0;
ListNode ans = new ListNode();
while (r1 != null || r2 != null) {
if (r1 != null) {
totalSum += r1.val;
r1 = r1.next;
}
if (r2 != null) {
totalSum += r2.val;
r2 = r2.next;
}
ans.val = totalSum % 10;
carry = totalSum / 10;
ListNode head = new ListNode(carry);
head.next = ans;
ans = head;
totalSum = carry;
}
return carry == 0 ? ans.next: ans;
}
}
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
prev = None
temp = None
while head:
# Keep the next node
temp = head.next
# Reverse the link
head.next = prev
# Update the previous node and the current node.
prev = head
head = temp
return prev
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
r1 = self.reverseList(l1)
r2 = self.reverseList(l2)
total_sum = 0
carry = 0
ans = ListNode()
while r1 or r2:
if r1:
total_sum += r1.val
r1 = r1.next
if r2:
total_sum += r2.val
r2 = r2.next
ans.val = total_sum % 10
carry = total_sum // 10
head = ListNode(carry)
head.next = ans
ans = head
total_sum = carry
return ans.next if carry == 0 else ans
Complexity Analysis
Time Complexity:
Reason:
- Reversing the list l1 and l2 take O(m) and O(n) time respectively.
- We then iterate over digits of the both lists. We iterate until both the lists are fully traversed. We iterate in the while loop max(m, n) times. We compute totalSum, carry and create a new node in each iteration which takes O(1) time. Hence, the complexity of all the while loop can be written as O(m+n) time.
Space Complexity:
Reason: As we have reversed the input linked lists, we will count the space consumed by the reversed lists. The r1 linked list takes O(m) space and r2 takes O(n) space.
Approach 2: Stack
Intuition
Our task is to do a basic addition of two numbers starting with the least significant digits and working our way up to the most significant digits. In the previous approach, we reversed the linked lists to access the least significant digits first. We can also use stacks to access the least significant digits first.
The advantage of using a stack is that when we loop over a given linked list from the first node to the last and push all the digits in the stack, the top of the stack will have the least significant digit and the bottom will contain the most significant digit.
We can add the digits at corresponding places of the linked lists using the two stacks moving from the least to the most significant digits using the stack's pop method.
Here's a brief visual representation explaining the approach:
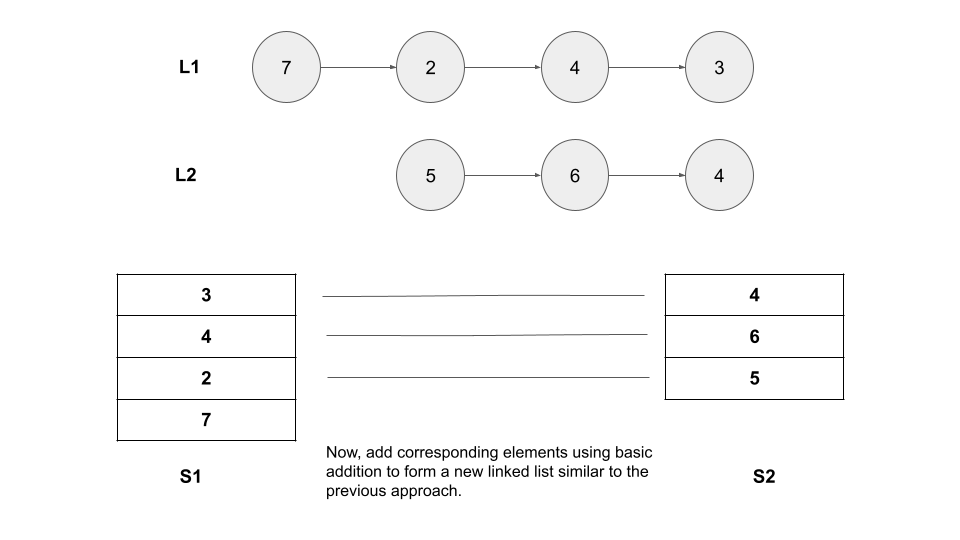
Algorithm
- Create two integer stacks
s1ands2to store the integers of the linked listsl1andl2respectively. - Push all the integers of
l1ins1starting from the integer at the first node. The most significant comes first in the list, so it will be stored at the bottom of the stack and the least significant digit will stored at the top. - Similarly, push all the integers of
l2ins2. - Create two integers
totalSumandcarryto store the sum and carry of current digits. - Create a new
ListNode,ansthat will store the answer. - We will add the two numbers present in the linked list now by adding the digits one by one. We continue until both
s1ands2are empty:- If
s1is not empty, pop the first element from the stack and add it tototalSum. - If
s2is not empty, pop the first element from the stack and add it tototalSum. - Set
ans.val = totalSum % 10. - Store the
carryastotalSum / 10. - Create a new
ListNode,newNodethat will havevalascarry. SetnextofnewNodetoans. Updateans = newNodeto use the same variableansfor the next iteration. - Update
totalSum = carry.
- If
- If
carry == 0, it means thenewNodethat we created in the final iteration of while loop hasval = 0. Because we performans = newNodeat the end of each while loop, to avoid returning a linked list with a head of0(leading zero), we return the next element, i.e., we returnans.next. Otherwise, ifcarryis not equal to0, the value ofansis non-zero. Hence, we just returnans.
Code in Different Languages
- C++
- Java
- Python
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
stack<int> s1, s2;
while (l1 != nullptr) {
s1.push(l1->val);
l1 = l1->next;
}
while (l2 != nullptr) {
s2.push(l2->val);
l2 = l2->next;
}
int totalSum = 0, carry = 0;
ListNode* ans = new ListNode();
while (!s1.empty() || !s2.empty()) {
if (!s1.empty()) {
totalSum += s1.top();
s1.pop();
}
if (!s2.empty()) {
totalSum += s2.top();
s2.pop();
}
ans->val = totalSum % 10;
carry = totalSum / 10;
ListNode* newNode = new ListNode(carry);
newNode->next = ans;
ans = newNode;
totalSum = carry;
}
return carry == 0 ? ans->next : ans;
}
};
public class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
Stack<Integer> s1 = new Stack<Integer>();
Stack<Integer> s2 = new Stack<Integer>();
while(l1 != null) {
s1.push(l1.val);
l1 = l1.next;
};
while(l2 != null) {
s2.push(l2.val);
l2 = l2.next;
}
int totalSum = 0, carry = 0;
ListNode ans = new ListNode();
while (!s1.empty() || !s2.empty()) {
if (!s1.empty()) {
totalSum += s1.pop();
}
if (!s2.empty()) {
totalSum += s2.pop();
}
ans.val = totalSum % 10;
carry = totalSum / 10;
ListNode head = new ListNode(carry);
head.next = ans;
ans = head;
totalSum = carry;
}
return carry == 0 ? ans.next: ans;
}
}
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
s1 = []
s2 = []
while l1:
s1.append(l1.val)
l1 = l1.next
while l2:
s2.append(l2.val)
l2 = l2.next
total_sum = 0
carry = 0
ans = ListNode()
while s1 or s2:
if s1:
total_sum += s1.pop()
if s2:
total_sum += s2.pop()
ans.val = total_sum % 10
carry = total_sum // 10
head = ListNode(carry)
head.next = ans
ans = head
total_sum = carry
return ans.next if carry == 0 else ans
Complexity Analysis
Time Complexity:
Reason:
- Iterating over both the lists and pushing all the values in the respective stacks take O(m+n) time.
- We then iterate over digits of the both lists. We iterate until both the stacks are empty. We iterate in the while loop max(m, n) times. We compute sum, carry and create a new node in each iteration which takes O(1) time. Hence, the complexity of all the while loop can be written as O(m+n) time.
Space Complexity:
Reason: The s1 stack takes O(m) space and the s2 stack takes O(n) space.
References
-
LeetCode Problem: Add Two Numbers II
-
Solution Link: Add Two Numbers II