Naive Pattern Matching Algorithm (Geeks for Geeks)

1. What is the Naive Pattern Matching Algorithm?

The Naive Pattern Matching algorithm is a straightforward approach for finding occurrences of a pattern string within a text string. It compares the pattern to each substring of the text and checks for a match.

2. Algorithm for Naive Pattern Matching

1. Loop through the text, and for each position in the text, check if the pattern matches the substring starting at that position.
2. If a match is found, record the starting index of the match.

3. How does the Naive Pattern Matching Algorithm work?

• For each position in the text, compare the substring of the text starting at that position with the pattern.
• If the pattern matches the substring, record the starting index.
• Continue this process until the end of the text is reached.

4. Problem Description

Given a text string and a pattern string, implement the Naive Pattern Matching algorithm to find all occurrences of the pattern in the text.

5. Examples

Example 1:

Input: text = "THIS IS A TEST TEXT", pattern = "TEST"
Output: Pattern found at index 10

Example 2:

Input: text = "AABAACAADAABAABA", pattern = "AABA"
Output: Pattern found at index 0, Pattern found at index 9, Pattern found at index 12

Explanation of Example 1:

• The pattern "TEST" is found in the text "THIS IS A TEST TEXT" at index 10.

Visual Example

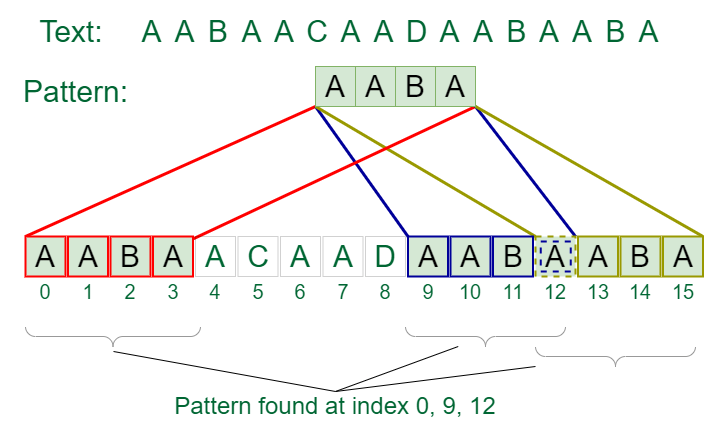
6. Constraints

• The text and pattern can contain any number of characters.
• All characters are $ASCII$ characters.

7. Implementation

Python

Written by GeeksforGeeks

def naive_pattern_search(text, pattern):
    n = len(text)
    m = len(pattern)
    
    for i in range(n - m + 1):
        j = 0
        while j < m and text[i + j] == pattern[j]:
            j += 1
        if j == m:
            print(f"Pattern found at index {i}")

# Example usage
text = "THIS IS A TEST TEXT"
pattern = "TEST"
naive_pattern_search(text, pattern)

text = "AABAACAADAABAABA"
pattern = "AABA"
naive_pattern_search(text, pattern)

C++

Written by GeeksforGeeks

#include <iostream>
#include <string>
using namespace std;

void naivePatternSearch(string txt, string pat) {
    int n = txt.size();
    int m = pat.size();

    for (int i = 0; i <= n - m; i++) {
        int j;
        for (j = 0; j < m; j++)
            if (txt[i + j] != pat[j])
                break;

        if (j == m)
            cout << "Pattern found at index " << i << endl;
    }
}

int main() {
    string txt = "THIS IS A TEST TEXT";
    string pat = "TEST";
    naivePatternSearch(txt, pat);

    txt = "AABAACAADAABAABA";
    pat = "AABA";
    naivePatternSearch(txt, pat);
    return 0;
}

Java

Written by GeeksforGeeks

public class NaivePatternMatching {
    static void naivePatternSearch(String txt, String pat) {
        int n = txt.length();
        int m = pat.length();

        for (int i = 0; i <= n - m; i++) {
            int j;
            for (j = 0; j < m; j++)
                if (txt.charAt(i + j) != pat.charAt(j))
                    break;

            if (j == m)
                System.out.println("Pattern found at index " + i);
        }
    }

    public static void main(String[] args) {
        String txt = "THIS IS A TEST TEXT";
        String pat = "TEST";
        naivePatternSearch(txt, pat);

        txt = "AABAACAADAABAABA";
        pat = "AABA";
        naivePatternSearch(txt, pat);
    }
}

JavaScript

Written by GeeksforGeeks

function naivePatternSearch(txt, pat) {
    const n = txt.length;
    const m = pat.length;

    for (let i = 0; i <= n - m; i++) {
        let j;
        for (j = 0; j < m; j++) {
            if (txt[i + j] !== pat[j]) {
                break;
            }
        }
        if (j === m) {
            console.log(`Pattern found at index ${i}`);
        }
    }
}

// Example usage:
let text = "THIS IS A TEST TEXT";
let pattern = "TEST";
naivePatternSearch(text, pattern);

text = "AABAACAADAABAABA";
pattern = "AABA";
naivePatternSearch(text, pattern);

8. Complexity Analysis

• Time Complexity:

  • Worst-case: $O((n-m+1) \cdot m)$, where $n$ is the length of the text and $m$ is the length of the pattern.
  • Best-case: $O(n - m + 1)$ when all characters of the pattern are different.

• Space Complexity: $O(1)$ as it uses a constant amount of extra space.

9. Advantages and Disadvantages

Advantages:

• Simple and easy to understand and implement.
• No preprocessing required.

Disadvantages:

• Inefficient for large texts and patterns with many repeated characters.
• Higher time complexity compared to more advanced algorithms like Boyer-Moore and KMP.

10. References

• GFG Problem: GFG Problem
• HackerRank Problem: HackerRank
• Author's Geeks for Geeks Profile: GeeksforGeeks