Manacher's Algorithm (Geeks for Geeks)

1. What is Manacher's Algorithm?

Manacher's Algorithm is an efficient algorithm used to find the longest palindromic substring in a given string. It operates in linear time, making it significantly faster than the traditional approach which operates in quadratic time.

2. Algorithm for Manacher's Algorithm

1. Preprocess the string to handle even-length palindromes by inserting a unique character (e.g., #) between every character and at the boundaries.
2. Use the preprocessed string to compute the length of the palindromes centered at each character using a palindrome expansion approach.
3. Track the maximum length palindrome and its center to determine the longest palindromic substring.

3. How does Manacher's Algorithm work?

• Preprocessing: Convert the string s to a new string t by inserting a unique character # between each character of s and adding boundary characters at the start and end.
• Palindrome Expansion: Use the preprocessed string t to compute an array p where p[i] gives the length of the palindrome centered at t[i].
• Longest Palindromic Substring: Find the maximum value in the array p to get the longest palindromic substring in the original string s.

4. Problem Description

Given a text string, implement Manacher's Algorithm to find the longest palindromic substring.

5. Examples

Example 1:

Input: text = "babad"
Output: "bab" (or "aba")

Example 2:

Input: text = "cbbd"
Output: "bb"

Explanation of Example 1:

• The longest palindromic substring in "babad" is "bab" or "aba".

Visual Example

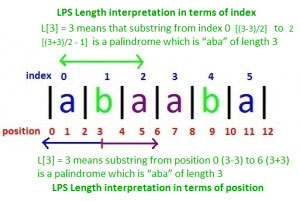
6. Constraints

• The text can contain any number of characters.
• All characters are $ASCII$ characters.

7. Implementation

Python

Written by @Anurag Singh

def preprocess(s):
    return '#' + '#'.join(s) + '#'

def manachers_algorithm(s):
    t = preprocess(s)
    n = len(t)
    p = [0] * n
    c = 0
    r = 0
    for i in range(n):
        mirr = 2 * c - i
        if i < r:
            p[i] = min(r - i, p[mirr])
        while i + p[i] + 1 < n and i - p[i] - 1 >= 0 and t[i + p[i] + 1] == t[i - p[i] - 1]:
            p[i] += 1
        if i + p[i] > r:
            c = i
            r = i + p[i]
    max_len = max(p)
    center_index = p.index(max_len)
    start = (center_index - max_len) // 2
    return s[start:start + max_len]

# Example usage:
text = "babad"
result = manachers_algorithm(text)
print("Longest Palindromic Substring:", result)

C++

Written by @Anurag Singh

#include <iostream>
#include <vector>
using namespace std;

string preprocess(const string &s) {
    string t = "#";
    for (char c : s) {
        t += c;
        t += "#";
    }
    return t;
}

string manachers_algorithm(const string &s) {
    string t = preprocess(s);
    int n = t.size();
    vector<int> p(n, 0);
    int c = 0, r = 0;
    for (int i = 0; i < n; i++) {
        int mirr = 2 * c - i;
        if (i < r)
            p[i] = min(r - i, p[mirr]);
        while (i + p[i] + 1 < n && i - p[i] - 1 >= 0 && t[i + p[i] + 1] == t[i - p[i] - 1])
            p[i]++;
        if (i + p[i] > r) {
            c = i;
            r = i + p[i];
        }
    }
    int max_len = 0, center_index = 0;
    for (int i = 0; i < n; i++) {
        if (p[i] > max_len) {
            max_len = p[i];
            center_index = i;
        }
    }
    int start = (center_index - max_len) / 2;
    return s.substr(start, max_len);
}

// Example usage:
int main() {
    string text = "babad";
    string result = manachers_algorithm(text);
    cout << "Longest Palindromic Substring: " << result << endl;
    return 0;
}

Java

Written by @Anurag Singh

public class ManachersAlgorithm {

    private static String preprocess(String s) {
        StringBuilder t = new StringBuilder("#");
        for (char c : s.toCharArray()) {
            t.append(c).append("#");
        }
        return t.toString();
    }

    public static String manachersAlgorithm(String s) {
        String t = preprocess(s);
        int n = t.length();
        int[] p = new int[n];
        int c = 0, r = 0;
        for (int i = 0; i < n; i++) {
            int mirr = 2 * c - i;
            if (i < r) {
                p[i] = Math.min(r - i, p[mirr]);
            }
            while (i + p[i] + 1 < n && i - p[i] - 1 >= 0 && t.charAt(i + p[i] + 1) == t.charAt(i - p[i] - 1)) {
                p[i]++;
            }
            if (i + p[i] > r) {
                c = i;
                r = i + p[i];
            }
        }
        int max_len = 0, center_index = 0;
        for (int i = 0; i < n; i++) {
            if (p[i] > max_len) {
                max_len = p[i];
                center_index = i;
            }
        }
        int start = (center_index - max_len) / 2;
        return s.substring(start, start + max_len);
    }

    // Example usage:
    public static void main(String[] args) {
        String text = "babad";
        String result = manachersAlgorithm(text);
        System.out.println("Longest Palindromic Substring: " + result);
    }
}

JavaScript

Written by @Anurag Singh

function preprocess(s) {
    return '#' + s.split('').join('#') + '#';
}

function manachersAlgorithm(s) {
    const t = preprocess(s);
    const n = t.length;
    const p = new Array(n).fill(0);
    let c = 0, r = 0;
    for (let i = 0; i < n; i++) {
        const mirr = 2 * c - i;
        if (i < r) {
            p[i] = Math.min(r - i, p[mirr]);
        }
        while (i + p[i] + 1 < n && i - p[i] - 1 >= 0 && t[i + p[i] + 1] === t[i - p[i] - 1]) {
            p[i]++;
        }
        if (i + p[i] > r) {
            c = i;
            r = i + p[i];
        }
    }
    let maxLen = 0;
    let centerIndex = 0;
    for (let i = 0; i < n; i++) {
        if (p[i] > maxLen) {
            maxLen = p[i];
            centerIndex = i;
        }
    }
    const start = (centerIndex - maxLen) / 2;
    return s.substring(start, start + maxLen);
}

// Example usage:
const text = "babad";
const result = manachersAlgorithm(text);
console.log("Longest Palindromic Substring:", result);

8. Complexity Analysis

• Time Complexity: $O(n)$, where $n$ is the length of the preprocessed string.
• Space Complexity: $O(n)$ for the arrays used.

9. Advantages and Disadvantages

Advantages:

• Linear time complexity.
• Efficient for finding the longest palindromic

substring.

Disadvantages:

• Requires preprocessing which increases the space complexity.

10. References

• GFG Problem: GFG Problem
• Author's Geeks for Geeks Profile: Anurag Singh