Knuth-Morris-Pratt (KMP) Algorithm (Geeks for Geeks)

1. What is the Knuth-Morris-Pratt (KMP) Algorithm?

The Knuth-Morris-Pratt (KMP) algorithm is an efficient pattern matching algorithm that searches for occurrences of a $word$ $W$ within a main $text string$ $T$ by employing the observation that when a mismatch occurs, the word itself embodies sufficient information to determine where the next match could begin, thus bypassing re-examination of previously matched characters.

2. Algorithm for Knuth-Morris-Pratt (KMP)

1. Preprocess the pattern to create an array (LPS array) that stores the length of the longest prefix which is also a suffix.
2. Use the $LPS array$ to skip characters while matching.

3. How does the Knuth-Morris-Pratt (KMP) Algorithm work?

• The KMP algorithm preprocesses the pattern to determine the longest prefix which is also a suffix in the pattern itself.
• This preprocessing is used to avoid unnecessary re-evaluation of the characters in the text, making the search process more efficient.

4. Problem Description

Given a text string and a pattern string, implement the $Knuth-Morris-Pratt (KMP)$ algorithm to find all occurrences of the pattern in the text.

5. Examples

Example 1:

Input: text = "ABABDABACDABABCABAB", pattern = "ABABCABAB"
Output: Pattern found at index 10

Example 2:

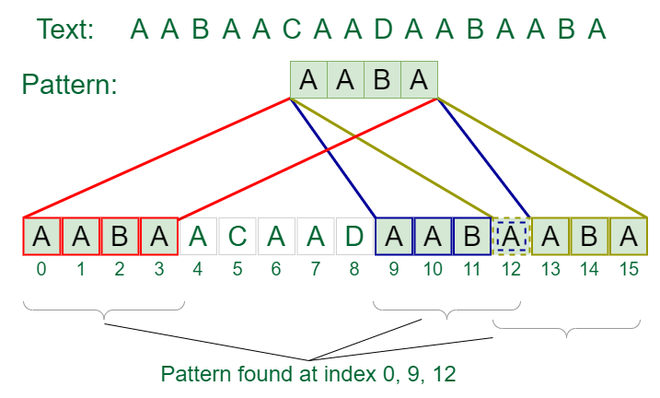
Input: text = "AABAACAADAABAABA", pattern = "AABA"
Output: Pattern found at index 0, Pattern found at index 9, Pattern found at index 12

Explanation of Example 1:

• The pattern "ABABCABAB" is found in the text "ABABDABACDABABCABAB" starting from index 10.

Visual Example

6. Constraints

• The text and pattern can contain any number of characters.
• All characters are $ASCII$ characters.

7. Implementation

Python

Written by @ngmuraqrdd

def KMPSearch(pat, txt):
    M = len(pat)
    N = len(txt)

    lps = [0] * M
    j = 0

    computeLPSArray(pat, M, lps)

    i = 0
    while i < N:
        if pat[j] == txt[i]:
            i += 1
            j += 1

        if j == M:
            print("Found pattern at index " + str(i - j))
            j = lps[j - 1]
        elif i < N and pat[j] != txt[i]:
            if j != 0:
                j = lps[j - 1]
            else:
                i += 1

def computeLPSArray(pat, M, lps):
    length = 0
    lps[0] = 0
    i = 1

    while i < M:
        if pat[i] == pat[length]:
            length += 1
            lps[i] = length
            i += 1
        else:
            if length != 0:
                length = lps[length - 1]
            else:
                lps[i] = 0
                i += 1

# Example usage:
text = "ABABDABACDABABCABAB"
pattern = "ABABCABAB"
KMPSearch(pattern, text)

C++

Written by @ngmuraqrdd

#include <iostream>
#include <vector>
using namespace std;

void computeLPSArray(string pat, int M, vector<int>& lps) {
    int length = 0;
    lps[0] = 0;
    int i = 1;

    while (i < M) {
        if (pat[i] == pat[length]) {
            length++;
            lps[i] = length;
            i++;
        } else {
            if (length != 0) {
                length = lps[length - 1];
            } else {
                lps[i] = 0;
                i++;
            }
        }
    }
}

void KMPSearch(string pat, string txt) {
    int M = pat.size();
    int N = txt.size();

    vector<int> lps(M);
    computeLPSArray(pat, M, lps);

    int i = 0;
    int j = 0;
    while (i < N) {
        if (pat[j] == txt[i]) {
            i++;
            j++;
        }

        if (j == M) {
            cout << "Found pattern at index " << (i - j) << endl;
            j = lps[j - 1];
        } else if (i < N && pat[j] != txt[i]) {
            if (j != 0) {
                j = lps[j - 1];
            } else {
                i++;
            }
        }
    }
}

int main() {
    string txt = "ABABDABACDABABCABAB";
    string pat = "ABABCABAB";
    KMPSearch(pat, txt);
    return 0;
}

Java

Written by @ngmuraqrdd

public class KMPAlgorithm {
    void KMPSearch(String pat, String txt) {
        int M = pat.length();
        int N = txt.length();

        int lps[] = new int[M];
        int j = 0;

        computeLPSArray(pat, M, lps);

        int i = 0;
        while (i < N) {
            if (pat.charAt(j) == txt.charAt(i)) {
                i++;
                j++;
            }
            if (j == M) {
                System.out.println("Found pattern at index " + (i - j));
                j = lps[j - 1];
            } else if (i < N && pat.charAt(j) != txt.charAt(i)) {
                if (j != 0)
                    j = lps[j - 1];
                else
                    i++;
            }
        }
    }

    void computeLPSArray(String pat, int M, int lps[]) {
        int len = 0;
        int i = 1;
        lps[0] = 0;

        while (i < M) {
            if (pat.charAt(i) == pat.charAt(len)) {
                len++;
                lps[i] = len;
                i++;
            } else {
                if (len != 0) {
                    len = lps[len - 1];
                } else {
                    lps[i] = 0;
                    i++;
                }
            }
        }
    }

    public static void main(String args[]) {
        String txt = "ABABDABACDABABCABAB";
        String pat = "ABABCABAB";
        new KMPAlgorithm().KMPSearch(pat, txt);
    }
}

JavaScript

Written by @ngmuraqrdd

function KMPSearch(pat, txt) {
    const M = pat.length;
    const N = txt.length;

    const lps = new Array(M).fill(0);
    computeLPSArray(pat, M, lps);

    let i = 0;
    let j = 0;
    while (i < N) {
        if (pat[j] === txt[i]) {
            i++;
            j++;
        }
        if (j === M) {
            console.log("Found pattern at index " + (i - j));
            j = lps[j - 1];
        } else if (i < N && pat[j] !== txt[i]) {
            if (j !== 0) {
                j = lps[j - 1];
            } else {
                i++;
            }
        }
    }
}

function computeLPSArray(pat, M, lps) {
    let length = 0;
    let i = 1;

    lps[0] = 0;

    while (i < M) {
        if (pat[i] === pat[length]) {
            length++;
            lps[i] = length;
            i++;
        } else {
            if (length !== 0) {
                length = lps[length - 1];
            } else {
                lps[i] = 0;
                i++;
            }
        }
    }
}

// Example usage:
const text = "ABABDABACDABABCABAB";
const

pattern = "ABABCABAB";
KMPSearch(pattern, text);

8. Complexity Analysis

• Time Complexity:

  • Preprocessing the LPS array: $O(M)$
  • Searching the pattern in the text: $O(N)$
  • Overall: $O(M + N)$

• Space Complexity: $O(M)$ for the LPS array.

9. Advantages and Disadvantages

Advantages:

• More efficient than the naive pattern matching algorithm, especially for large texts.
• Avoids redundant comparisons.

Disadvantages:

• Slightly more complex to implement than naive algorithms.
• Requires additional space for the LPS array.

10. References

• GFG Problem: GFG Problem
• HackerRank Problem: HackerRank
• Author's Geeks for Geeks Profile: MuraliDharan