Maximum Product of the Length of Two Palindromic Subsequences

Problem Description

Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.

Return the maximum possible product of the lengths of the two palindromic subsequences.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.

Examples

Example 1:

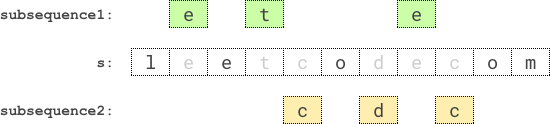
Input: s = "leetcodecom"
Output: 9
Explanation: An optimal solution is to choose "ete" for the 1st subsequence and "cdc" for the 2nd subsequence.
The product of their lengths is: 3 * 3 = 9.

Example 2:

Input: s = "accbcaxxcxx"
Output: 25
Explanation: An optimal solution is to choose "accca" for the 1st subsequence and "xxcxx" for the 2nd subsequence.
The product of their lengths is: 5 * 5 = 25.

Constraints

• 2 <= s.length <= 12
• s consists of lowercase English letters only.

Solution for Maximum Product of the Length of Two Palindromic Subsequences

1. Generate All Subsequences:

   • The function sub recursively generates all subsequences of the input string s.
   • For each subsequence, it checks if it is a palindrome using the isPalindrome function.
   • If a subsequence is a palindrome, it is added to the global result list ans.

2. Check Palindromes:

   • The function isPalindrome takes a string and a list of indices (subsequence) and checks if the characters at these indices form a palindrome.

3. Check Non-overlapping Subsequences:

   • The function check takes two subsequences and checks if they have any common elements (indices).
   • If they don't share any indices, they are considered non-overlapping.

4. Calculate Maximum Product:

   • The function maxProduct iterates through all pairs of palindromic subsequences.
   • For each pair, it checks if they are non-overlapping using the check function.
   • If they are non-overlapping, it calculates the product of their lengths and updates the maximum product found.

Intuition

• The idea is to find all palindromic subsequences and then determine the maximum product of the lengths of two non-overlapping palindromic subsequences.
• Generating all subsequences ensures that no potential palindromic subsequences are missed.
• Checking for non-overlapping ensures that the two subsequences do not share any characters, thus making the product calculation valid.

Solution

Implementation

Live Editor

function Solution(arr) {
        const ans = [];

    function isPalindrome(s, ans) {
        let a = 0, b = ans.length - 1;
        while (a <= b) {
            if (s[ans[a]] !== s[ans[b]]) return false;
            a++;
            b--;
        }
        return true;
    }

    function check(a, b) {
        for (let i = 0; i < a.length; i++) {
            for (let j = 0; j < b.length; j++) {
                if (a[i] === b[j]) return false;
            }
        }
        return true;
    }

    function sub(nums, i, temp) {
        if (isPalindrome(nums, temp)) ans.push([...temp]);
        if (i >= nums.length) return;

        temp.push(i);
        sub(nums, i + 1, temp);

        temp.pop();
        sub(nums, i + 1, temp);
    }

    function maxProduct(s) {
        const temp = [];
        sub(s, 0, temp);
        let res = 0;
        for (let i = 0; i < ans.length; i++) {
            for (let j = i + 1; j < ans.length; j++) {
                let x = ans[i].length * ans[j].length;
                if (check(ans[i], ans[j])) {
                    res = Math.max(res, x);
                }
            }
        }
        return res;
    }

  const input = "leetcodecom"
  const output = maxProduct(input)
  return (
    <div>
      <p>
        <b>Input: </b>
        {JSON.stringify(input)}
      </p>
      <p>
        <b>Output:</b> {output.toString()}
      </p>
    </div>
  );
}

Result

Loading...

Complexity Analysis

• Time Complexity: $O(n * 4^n)$
• Space Complexity: $O(n * 2^n)$

Code in Different Languages

JavaScript

Written by @hiteshgahanolia

const ans = [];

function isPalindrome(s, ans) {
 let a = 0, b = ans.length - 1;
 while (a <= b) {
     if (s[ans[a]] !== s[ans[b]]) return false;
     a++;
     b--;
 }
 return true;
}

function check(a, b) {
 for (let i = 0; i < a.length; i++) {
     for (let j = 0; j < b.length; j++) {
         if (a[i] === b[j]) return false;
     }
 }
 return true;
}

function sub(nums, i, temp) {
 if (isPalindrome(nums, temp)) ans.push([...temp]);
 if (i >= nums.length) return;

 temp.push(i);
 sub(nums, i + 1, temp);

 temp.pop();
 sub(nums, i + 1, temp);
}

function maxProduct(s) {
 const temp = [];
 sub(s, 0, temp);
 let res = 0;
 for (let i = 0; i < ans.length; i++) {
     for (let j = i + 1; j < ans.length; j++) {
         let x = ans[i].length * ans[j].length;
         if (check(ans[i], ans[j])) {
             res = Math.max(res, x);
         }
     }
 }
 return res;
}

TypeScript

Written by @hiteshgahanolia

class Solution {
 ans: number[][] = [];

 isPalindrome(s: string, ans: number[]): boolean {
     let a = 0, b = ans.length - 1;
     while (a <= b) {
         if (s[ans[a]] !== s[ans[b]]) return false;
         a++;
         b--;
     }
     return true;
 }

 check(a: number[], b: number[]): boolean {
     for (let i = 0; i < a.length; i++) {
         for (let j = 0; j < b.length; j++) {
             if (a[i] === b[j]) return false;
         }
     }
     return true;
 }

 sub(nums: string, i: number, temp: number[]): void {
     if (this.isPalindrome(nums, temp)) this.ans.push([...temp]);
     if (i >= nums.length) return;

     temp.push(i);
     this.sub(nums, i + 1, temp);

     temp.pop();
     this.sub(nums, i + 1, temp);
 }

 maxProduct(s: string): number {
     let temp: number[] = [];
     this.sub(s, 0, temp);
     let res = 0;
     for (let i = 0; i < this.ans.length; i++) {
         for (let j = i + 1; j < this.ans.length; j++) {
             let x = this.ans[i].length * this.ans[j].length;
             if (this.check(this.ans[i], this.ans[j])) {
                 res = Math.max(res, x);
             }
         }
     }
     return res;
 }
}

Python

Written by @hiteshgahanolia

class Solution:
 def __init__(self):
     self.ans = []

 def isPalindrome(self, s, ans):
     a, b = 0, len(ans) - 1
     while a <= b:
         if s[ans[a]] != s[ans[b]]:
             return False
         a += 1
         b -= 1
     return True

 def check(self, a, b):
     for i in a:
         for j in b:
             if i == j:
                 return False
     return True

 def sub(self, nums, i, temp):
     if self.isPalindrome(nums, temp):
         self.ans.append(temp[:])
     if i >= len(nums):
         return

     temp.append(i)
     self.sub(nums, i + 1, temp)

     temp.pop()
     self.sub(nums, i + 1, temp)

 def maxProduct(self, s):
     temp = []
     self.sub(s, 0, temp)
     res = 0
     for i in range(len(self.ans)):
         for j in range(i + 1, len(self.ans)):
             x = len(self.ans[i]) * len(self.ans[j])
             if self.check(self.ans[i], self.ans[j]):
                 res = max(res, x)
     return res

Java

Written by @hiteshgahanolia

import java.util.ArrayList;
import java.util.List;

class Solution {
 public List<List<Integer>> ans = new ArrayList<>();

 public boolean isPalindrome(String s, List<Integer> ans) {
     int a = 0, b = ans.size() - 1;
     while (a <= b) {
         if (s.charAt(ans.get(a)) != s.charAt(ans.get(b)))
             return false;
         a++;
         b--;
     }
     return true;
 }

 public boolean check(List<Integer> a, List<Integer> b) {
     for (int i = 0; i < a.size(); i++)
         for (int j = 0; j < b.size(); j++)
             if (a.get(i).equals(b.get(j)))
                 return false;
     return true;
 }

 public void sub(String nums, int i, List<Integer> temp) {
     if (isPalindrome(nums, temp))
         ans.add(new ArrayList<>(temp));
     if (i >= nums.length()) {
         return;
     }

     temp.add(i);
     sub(nums, i + 1, temp);

     temp.remove(temp.size() - 1);
     sub(nums, i + 1, temp);
 }

 public int maxProduct(String s) {
     List<Integer> temp = new ArrayList<>();
     sub(s, 0, temp);
     int res = 0;
     for (int i = 0; i < ans.size(); i++) {
         for (int j = i + 1; j < ans.size(); j++) {
             int x = ans.get(i).size() * ans.get(j).size();
             if (check(ans.get(i), ans.get(j))) {
                 res = Math.max(res, x);
             }
         }
     }
     return res;
 }
}

C++

Written by @hiteshgahanolia

class Solution {
public:
 vector<vector<int>> ans;
 bool isPalindrome(string& s, vector<int>& ans) {
     int a = 0, b = ans.size() - 1;
     while (a <= b) {
         if (s[ans[a]] != s[ans[b]])
             return false;
         a++;
         b--;
     }
     return true;
 }

 bool check(vector<int>& a, vector<int>& b) {
     for (int i = 0; i < a.size(); i++)
         for (int j = 0; j < b.size(); j++)
             if (a[i] == b[j])
                 return false;
     return true;
 }

 void sub(string &nums, int i, vector<int>& temp) {
     if (isPalindrome(nums, temp))
         ans.push_back(temp);
     if (i >= nums.size()) {
         return;
     }

     temp.push_back(i);
     sub(nums, i + 1, temp);

     temp.pop_back();
     sub(nums, i + 1, temp);
 }

 int maxProduct(string s) {
     vector<int> temp;
     sub(s , 0 ,temp);
     int res = 0;
     for (int i = 0; i < ans.size(); i++) {
         for (int j = i + 1; j < ans.size(); j++) {
            int x = static_cast<int>(ans[i].size() * ans[j].size());
             if (check(ans[i], ans[j])) {
                 res = max(res, x);
             }
         }
     }
     return res;
 }
};

References

• LeetCode Problem: Maximum Product of the Length of Two Palindromic Subsequences

• Solution Link: LeetCode Solution