Nearest Exit from Entrance in Maze
Problem Description
You are given an m x n matrix maze (0-indexed) with empty cells (represented as '.') and walls (represented as '+'). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.
In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.
Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.
Examples
Example 1:
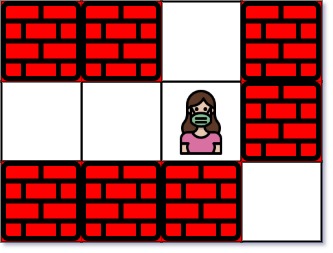
Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
Output: 1
Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3].
Initially, you are at the entrance cell [1,2].
- You can reach [1,0] by moving 2 steps left.
- You can reach [0,2] by moving 1 step up.
It is impossible to reach [2,3] from the entrance.
Thus, the nearest exit is [0,2], which is 1 step away.
Example 2:

Input: maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
Output: 2
Explanation: There is 1 exit in this maze at [1,2].
[1,0] does not count as an exit since it is the entrance cell.
Initially, you are at the entrance cell [1,0].
- You can reach [1,2] by moving 2 steps right.
Thus, the nearest exit is [1,2], which is 2 steps away.
Example 3:

Input: maze = [[".","+"]], entrance = [0,0]
Output: -1
Explanation: There are no exits in this maze.
Constraints
maze.length == mmaze[i].length == n1 <= m, n <= 100maze[i][j] is either '.' or '+'.entrance.length == 20 <= entrancerow < m0 <= entrancecol < nentrance will always be an empty cell.
Solution for Nearest Exit from Entrance in Maze Problem
Intuition
The problem requires finding the shortest path from an entrance in a maze to the nearest exit. An exit is defined as any cell on the boundary of the maze that is not the entrance itself. The maze consists of open paths represented by '.' and walls represented by '+'. The goal is to traverse the maze and determine the minimum number of steps required to reach an exit.
To solve this problem, we can use the Breadth-First Search (BFS) algorithm. BFS is particularly suitable for finding the shortest path in an unweighted grid because it explores all nodes at the present "depth" (or distance) before moving on to nodes at the next depth level.
Approach
-
Initialize Direction Vectors: Use direction vectors to facilitate movement in four possible directions (up, right, down, left).
-
Mark the Entrance as Visited: Create a visited matrix to keep track of visited cells. Mark the entrance cell as visited to avoid revisiting it.
-
Initialize BFS Queue: Use a queue to implement the BFS. Enqueue the entrance cell with its coordinates.
-
BFS Traversal:
- While the queue is not empty, iterate through each cell in the current level.
- For each cell, try moving to its neighboring cells (up, right, down, left) using the direction vectors.
- If a neighboring cell is within bounds, is not a wall, and has not been visited, mark it as visited and enqueue it.
- If the neighboring cell is on the boundary of the maze and is not the entrance, return the current distance as it represents the shortest path to an exit.
-
Return Result: If the BFS completes without finding an exit, return -1 to indicate that no exit is reachable.
- Solution
Implementation
function Solution(arr) { function nearestExit(maze, entrance) { const delRow = [-1, 0, 1, 0]; const delCol = [0, 1, 0, -1]; const n = maze.length; const m = maze[0].length; const vis = Array.from({ length: n }, () => Array(m).fill(0)); vis[entrance[0]][entrance[1]] = 1; const q = []; q.push([entrance[0], entrance[1]]); let move = 0; while (q.length > 0) { let size = q.length; move++; while (size-- > 0) { const [row, col] = q.shift(); for (let i = 0; i < 4; i++) { const newRow = row + delRow[i]; const newCol = col + delCol[i]; if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m && maze[newRow][newCol] !== '+' && vis[newRow][newCol] !== 1) { if (newRow === 0 || newRow === n - 1 || newCol === 0 || newCol === m - 1) return move; vis[newRow][newCol] = 1; q.push([newRow, newCol]); } } } } return -1; } const input = [["+","+","+"],[".",".","."],["+","+","+"]] const entrance = [1,0] const output = nearestExit(input , entrance) return ( <div> <p> <b>Input: </b> {JSON.stringify(input)} </p> <p> <b>Output:</b> {output.toString()} </p> </div> ); }
Complexity Analysis
- Time Complexity:
- Space Complexity:
Code in Different Languages
- JavaScript
- TypeScript
- Python
- Java
- C++
function nearestExit(maze, entrance) {
const delRow = [-1, 0, 1, 0];
const delCol = [0, 1, 0, -1];
const n = maze.length;
const m = maze[0].length;
const vis = Array.from({ length: n }, () => Array(m).fill(0));
vis[entrance[0]][entrance[1]] = 1;
const q = [];
q.push([entrance[0], entrance[1]]);
let move = 0;
while (q.length > 0) {
let size = q.length;
move++;
while (size-- > 0) {
const [row, col] = q.shift();
for (let i = 0; i < 4; i++) {
const newRow = row + delRow[i];
const newCol = col + delCol[i];
if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m && maze[newRow][newCol] !== '+' && vis[newRow][newCol] !== 1) {
if (newRow === 0 || newRow === n - 1 || newCol === 0 || newCol === m - 1) return move;
vis[newRow][newCol] = 1;
q.push([newRow, newCol]);
}
}
}
}
return -1;
}
function nearestExit(maze: string[][], entrance: number[]): number {
const delRow = [-1, 0, 1, 0];
const delCol = [0, 1, 0, -1];
const n = maze.length;
const m = maze[0].length;
const vis: number[][] = Array.from({ length: n }, () => Array(m).fill(0));
vis[entrance[0]][entrance[1]] = 1;
const q: [number, number][] = [];
q.push([entrance[0], entrance[1]]);
let move = 0;
while (q.length > 0) {
let size = q.length;
move++;
while (size-- > 0) {
const [row, col] = q.shift()!;
for (let i = 0; i < 4; i++) {
const newRow = row + delRow[i];
const newCol = col + delCol[i];
if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m && maze[newRow][newCol] !== '+' && vis[newRow][newCol] !== 1) {
if (newRow === 0 || newRow === n - 1 || newCol === 0 || newCol === m - 1) return move;
vis[newRow][newCol] = 1;
q.push([newRow, newCol]);
}
}
}
}
return -1;
}
from collections import deque
def nearest_exit(maze, entrance):
delRow = [-1, 0, 1, 0]
delCol = [0, 1, 0, -1]
n = len(maze)
m = len(maze[0])
vis = [[0] * m for _ in range(n)]
vis[entrance[0]][entrance[1]] = 1
q = deque([(entrance[0], entrance[1])])
move = 0
while q:
size = len(q)
move += 1
for _ in range(size):
row, col = q.popleft()
for i in range(4):
newRow = row + delRow[i]
newCol = col + delCol[i]
if 0 <= newRow < n and 0 <= newCol < m and maze[newRow][newCol] != '+' and vis[newRow][newCol] != 1:
if newRow == 0 or newRow == n - 1 or newCol == 0 or newCol == m - 1:
return move
vis[newRow][newCol] = 1
q.append((newRow, newCol))
return -1
import java.util.*;
class Solution {
public int nearestExit(char[][] maze, int[] entrance) {
int[] delRow = {-1, 0, 1, 0};
int[] delCol = {0, 1, 0, -1};
int n = maze.length, m = maze[0].length;
int[][] vis = new int[n][m];
vis[entrance[0]][entrance[1]] = 1;
Queue<int[]> q = new LinkedList<>();
q.add(new int[]{entrance[0], entrance[1]});
int move = 0;
while (!q.isEmpty()) {
int size = q.size();
move++;
while (size-- > 0) {
int[] current = q.poll();
int row = current[0];
int col = current[1];
for (int i = 0; i < 4; i++) {
int newRow = row + delRow[i];
int newCol = col + delCol[i];
if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m && maze[newRow][newCol] != '+' && vis[newRow][newCol] != 1) {
if (newRow == 0 || newRow == n - 1 || newCol == 0 || newCol == m - 1) return move;
vis[newRow][newCol] = 1;
q.add(new int[]{newRow, newCol});
}
}
}
}
return -1;
}
}
class Solution {
public:
int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
int delRow[] = {-1,0,+1,0};
int delCol[] = {0,1,0,-1};
queue<pair<int,int>>q;
int n = maze.size() , m = maze[0].size();
vector<vector<int>>vis(n,vector<int>(m,0));
vis[entrance[0]][entrance[1]]=1;
q.push({entrance[0],entrance[1]});
int move=0;
while(!q.empty())
{
int size=q.size();
move++;
while(size--)
{
int row=q.front().first;
int col=q.front().second;
q.pop();
for(int i=0;i<4;i++)
{
int newRow=row+delRow[i];
int newCol=col+delCol[i];
if(newRow>=0 && newRow<n && newCol>=0 && newCol<m && maze[newRow][newCol]!='+' && vis[newRow][newCol]!=1)
{
if(newRow==0 || newRow==n-1 || newCol==0 ||newCol==m-1) return move;
vis[newRow][newCol]=1;
q.push({newRow,newCol});
}
}
}
}
return -1;
}
};
References
-
LeetCode Problem: Nearest Exit from Entrance in Maze
-
Solution Link: LeetCode Solution