Path With Minimum Effort
Problem Description
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.
A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.
Return the minimum effort required to travel from the top-left cell to the bottom-right cell.
Examples
Example 1:
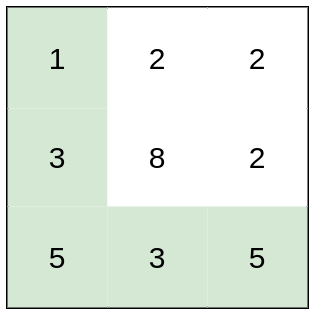
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
Example 2:
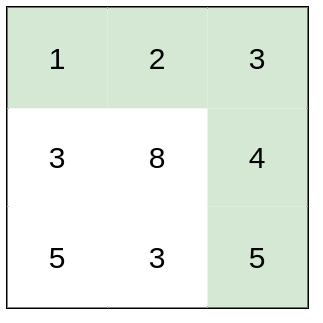
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
Example 3:
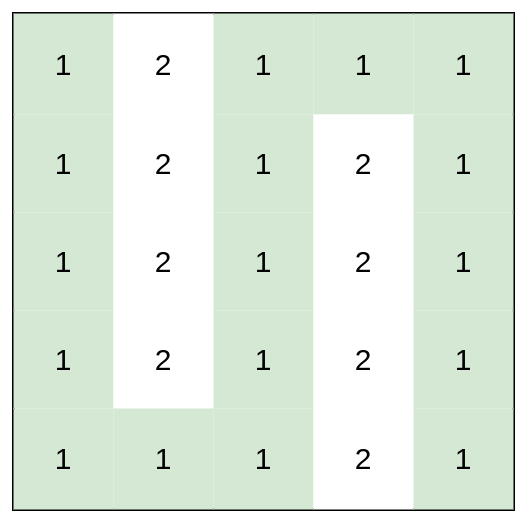
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.
Constraints
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 10^6
Solution for Path With Minimum Effort Problem
Approach
Dijkstra's Algorithm:
- A classic algorithm for finding the shortest path in a weighted graph, adapted for this problem.
Steps
Initialize Priority Queue:
- The algorithm starts at the top-left corner (the source). The priority queue is initialized to store the effort needed to reach each cell from the source. The effort for the source itself is zero.
Distance Matrix:
- A 2D array keeps track of the minimum effort required to reach each cell. Initially, this is set to infinity for all cells except the source.
Iterate and Update Distances:
- The algorithm pops the cell with the smallest effort from the priority queue and explores its neighbors. The effort required to reach a neighbor is updated if a smaller effort is found.
Early Exit:
- The algorithm stops when it reaches the bottom-right corner, returning the effort required to get there.
- Solution
Implementation
Live Editor
function Solution(arr) { function minimumEffortPath(heights) { const rows = heights.length, cols = heights[0].length; const dist = Array.from(Array(rows), () => Array(cols).fill(Infinity)); const minHeap = [[0, 0, 0]]; // [effort, x, y] dist[0][0] = 0; const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]]; while (minHeap.length > 0) { const [effort, x, y] = minHeap.shift(); if (effort > dist[x][y]) continue; if (x === rows - 1 && y === cols - 1) return effort; for (const [dx, dy] of directions) { const nx = x + dx, ny = y + dy; if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) { const newEffort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny])); if (newEffort < dist[nx][ny]) { dist[nx][ny] = newEffort; minHeap.push([newEffort, nx, ny]); minHeap.sort((a, b) => a[0] - b[0]); } } } } return -1; } const input = [[1,2,2],[3,8,2],[5,3,5]] const output = minimumEffortPath(input) ; return ( <div> <p> <b>Input: </b> {JSON.stringify(input)} </p> <p> <b>Output:</b> {output.toString()} </p> </div> ); }
Result
Loading...
Complexity Analysis
- Time Complexity: where M and N are the dimensions of the grid. This is primarily due to the operations on the priority queue.
- Space Complexity: , needed for the distance matrix and the priority queue.
Code in Different Languages
- JavaScript
- TypeScript
- Python
- Java
- C++
function minimumEffortPath(heights) {
const rows = heights.length, cols = heights[0].length;
const dist = Array.from(Array(rows), () => Array(cols).fill(Infinity));
const minHeap = [[0, 0, 0]]; // [effort, x, y]
dist[0][0] = 0;
const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];
while (minHeap.length > 0) {
const [effort, x, y] = minHeap.shift();
if (effort > dist[x][y]) continue;
if (x === rows - 1 && y === cols - 1) return effort;
for (const [dx, dy] of directions) {
const nx = x + dx, ny = y + dy;
if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {
const newEffort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny]));
if (newEffort < dist[nx][ny]) {
dist[nx][ny] = newEffort;
minHeap.push([newEffort, nx, ny]);
minHeap.sort((a, b) => a[0] - b[0]);
}
}
}
}
return -1;
}
class Solution {
minimumEffortPath(heights: number[][]): number {
const pq = new MinPriorityQueue<{priority: number, element: [number, [number, number]]}>({ priority: x => x.priority });
const n = heights.length;
const m = heights[0].length;
const dist = Array.from({ length: n }, () => Array(m).fill(Infinity));
dist[0][0] = 0;
pq.enqueue({priority: 0, element: [0, [0, 0]]});
const delRow = [-1, 0, 1, 0];
const delCol = [0, 1, 0, -1];
while (!pq.isEmpty()) {
const {element: [diff, [row, col]]} = pq.dequeue();
if (row === n - 1 && col === m - 1) return diff;
for (let i = 0; i < 4; i++) {
const newRow = row + delRow[i];
const newCol = col + delCol[i];
if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m) {
const newEffort = Math.max(Math.abs(heights[row][col] - heights[newRow][newCol]), diff);
if (newEffort < dist[newRow][newCol]) {
dist[newRow][newCol] = newEffort;
pq.enqueue({priority: newEffort, element: [newEffort, [newRow, newCol]]});
}
}
}
}
return 0;
}
}
import heapq
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
n, m = len(heights), len(heights[0])
dist = [[float('inf')] * m for _ in range(n)]
dist[0][0] = 0
pq = [(0, 0, 0)]
delRow = [-1, 0, 1, 0]
delCol = [0, 1, 0, -1]
while pq:
diff, row, col = heapq.heappop(pq)
if row == n - 1 and col == m - 1:
return diff
for i in range(4):
newRow, newCol = row + delRow[i], col + delCol[i]
if 0 <= newRow < n and 0 <= newCol < m:
newEffort = max(abs(heights[row][col] - heights[newRow][newCol]), diff)
if newEffort < dist[newRow][newCol]:
dist[newRow][newCol] = newEffort
heapq.heappush(pq, (newEffort, newRow, newCol))
return 0
import java.util.*;
class Solution {
public int minimumEffortPath(int[][] heights) {
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
int n = heights.length;
int m = heights[0].length;
int[][] dist = new int[n][m];
for (int[] row : dist) Arrays.fill(row, Integer.MAX_VALUE);
dist[0][0] = 0;
pq.offer(new int[]{0, 0, 0});
int[] delRow = {-1, 0, 1, 0};
int[] delCol = {0, 1, 0, -1};
while (!pq.isEmpty()) {
int[] curr = pq.poll();
int diff = curr[0];
int row = curr[1];
int col = curr[2];
if (row == n - 1 && col == m - 1) return diff;
for (int i = 0; i < 4; i++) {
int newRow = row + delRow[i];
int newCol = col + delCol[i];
if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m) {
int newEffort = Math.max(Math.abs(heights[row][col] - heights[newRow][newCol]), diff);
if (newEffort < dist[newRow][newCol]) {
dist[newRow][newCol] = newEffort;
pq.offer(new int[]{newEffort, newRow, newCol});
}
}
}
}
return 0;
}
}
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
priority_queue<pair<int, pair<int, int>>,
vector<pair<int, pair<int, int>>>,
greater<pair<int, pair<int, int>>>>pq;
int n = heights.size();
int m = heights[0].size();
vector<vector<int>> dist(n, vector<int>(m, 1e9));
dist[0][0] = 0;
// {diff{row,col}}
pq.push({0, {0, 0}});
int delRow[] = {-1, 0, 1, 0};
int delCol[] = {0, 1, 0, -1};
while (!pq.empty()) {
auto it = pq.top();
pq.pop();
int diff = it.first;
int row = it.second.first;
int col = it.second.second;
if (row == n - 1 && col == m - 1)
return diff;
for (int i = 0; i < 4; i++) {
int newRow = row + delRow[i];
int newCol = col + delCol[i];
if (newRow >= 0 & newRow < n && newCol >= 0 && newCol < m) {
int newEffort = max(
abs(heights[row][col] - heights[newRow][newCol]), diff);
;
if (newEffort < dist[newRow][newCol]) {
dist[newRow][newCol] = newEffort;
pq.push({newEffort, {newRow, newCol}});
}
}
}
}
return 0;
}
};
References
-
LeetCode Problem: Path With Minimum Effort
-
Solution Link: LeetCode Solution