Max Area of Island

Problem Description

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Examples

Example 1:

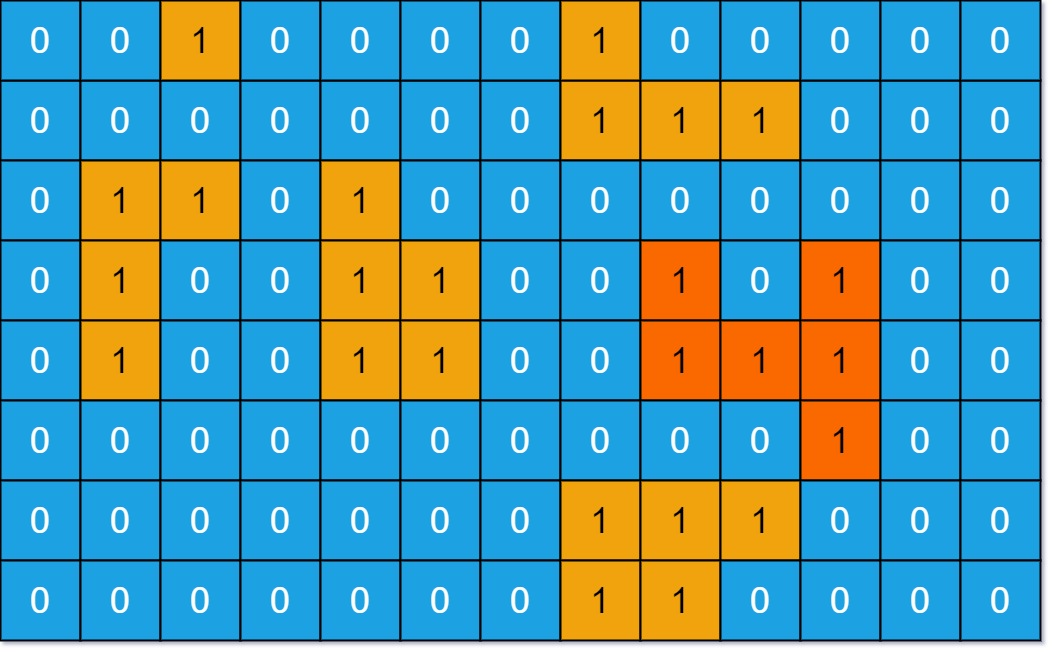
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0

Constraints

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] is either 0 or 1.

Solution for Max Area of Island

Approach 1: Depth-First Search (Recursive)

Intuition and Algorithm

We want to know the area of each connected shape in the grid, then take the maximum of these.

If we are on a land square and explore every square connected to it 4-directionally (and recursively squares connected to those squares, and so on), then the total number of squares explored will be the area of that connected shape.

To ensure we don't count squares in a shape more than once, let's use seen to keep track of squares we haven't visited before. It will also prevent us from counting the same shape more than once.

Code in Different Languages

Java

Written by @Shreyash3087

class Solution {
    int[][] grid;
    boolean[][] seen;

    public int area(int r, int c) {
        if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length ||
                seen[r][c] || grid[r][c] == 0)
            return 0;
        seen[r][c] = true;
        return (1 + area(r+1, c) + area(r-1, c)
                  + area(r, c-1) + area(r, c+1));
    }

    public int maxAreaOfIsland(int[][] grid) {
        this.grid = grid;
        seen = new boolean[grid.length][grid[0].length];
        int ans = 0;
        for (int r = 0; r < grid.length; r++) {
            for (int c = 0; c < grid[0].length; c++) {
                ans = Math.max(ans, area(r, c));
            }
        }
        return ans;
    }
}

Python

Written by @Shreyash3087

class Solution(object):
    def maxAreaOfIsland(self, grid):
        seen = set()
        def area(r, c):
            if not (0 <= r < len(grid) and 0 <= c < len(grid[0])
                    and (r, c) not in seen and grid[r][c]):
                return 0
            seen.add((r, c))
            return (1 + area(r+1, c) + area(r-1, c) +
                    area(r, c-1) + area(r, c+1))

        return max(area(r, c)
                   for r in range(len(grid))
                   for c in range(len(grid[0])))

Complexity Analysis

Time Complexity: $O(R \times C)$

Reason: where R is the number of rows in the given grid, and C is the number of columns. We visit every square once.

Space Complexity: $O(R \times C)$

Reason: the space used by seen to keep track of visited squares and the space used by the call stack during our recursion.

Approach 2: Depth-First Search (Iterative)

Intuition and Algorithm

We can try the same approach using a stack-based, (or "iterative") depth-first search.

Here, seen will represent squares that have either been visited or are added to our list of squares to visit (stack). For every starting land square that hasn't been visited, we will explore 4-directionally around it, adding land squares that haven't been added to seen to our stack.

On the side, we'll keep a count shape of the total number of squares seen during the exploration of this shape. We'll want the running max of these counts.

Code in Different Languages

Java

Written by @Shreyash3087

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        boolean[][] seen = new boolean[grid.length][grid[0].length];
        int[] dr = new int[]{1, -1, 0, 0};
        int[] dc = new int[]{0, 0, 1, -1};

        int ans = 0;
        for (int r0 = 0; r0 < grid.length; r0++) {
            for (int c0 = 0; c0 < grid[0].length; c0++) {
                if (grid[r0][c0] == 1 && !seen[r0][c0]) {
                    int shape = 0;
                    Stack<int[]> stack = new Stack();
                    stack.push(new int[]{r0, c0});
                    seen[r0][c0] = true;
                    while (!stack.empty()) {
                        int[] node = stack.pop();
                        int r = node[0], c = node[1];
                        shape++;
                        for (int k = 0; k < 4; k++) {
                            int nr = r + dr[k];
                            int nc = c + dc[k];
                            if (0 <= nr && nr < grid.length &&
                                    0 <= nc && nc < grid[0].length &&
                                    grid[nr][nc] == 1 && !seen[nr][nc]) {
                                stack.push(new int[]{nr, nc});
                                seen[nr][nc] = true;
                            }
                        }
                    }
                    ans = Math.max(ans, shape);
                }
            }
        }
        return ans;
    }
}

Python

Written by @Shreyash3087

class Solution(object):
    def maxAreaOfIsland(self, grid):
        seen = set()
        ans = 0
        for r0, row in enumerate(grid):
            for c0, val in enumerate(row):
                if val and (r0, c0) not in seen:
                    shape = 0
                    stack = [(r0, c0)]
                    seen.add((r0, c0))
                    while stack:
                        r, c = stack.pop()
                        shape += 1
                        for nr, nc in ((r-1, c), (r+1, c), (r, c-1), (r, c+1)):
                            if (0 <= nr < len(grid) and 0 <= nc < len(grid[0])
                                    and grid[nr][nc] and (nr, nc) not in seen):
                                stack.append((nr, nc))
                                seen.add((nr, nc))
                    ans = max(ans, shape)
        return ans

Complexity Analysis

Time Complexity: $O(R \times C)$

Reason: where R is the number of rows in the given grid, and C is the number of columns. We visit every square once.

Space Complexity: $O(R \times C)$

Reason: the space used by seen to keep track of visited squares and the space used by stack.

References

• LeetCode Problem: Max Area of Island

• Solution Link: Max Area of Island

---

Authors:

Loading...