Level Order Traversal

Problem Description

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Examples

Example 1:

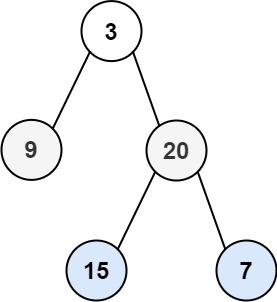
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Constraints

• The number of nodes in the tree is in the range [0, 2000].
• -1000 <= Node.val <= 1000

Solution for Binary Tree Level Order Traversal

Intuition

• To perform a level-order traversal on a binary tree and store the nodes’ values in a 2D vector representing each level, start by initialising an empty queue to hold the level by level nodes.Enqueue the root node into the queue and traverse until the queue is empty. For each level, track the number of nodes in that level, creating a temporary vector to deque and store them. At each node, store its value in the temporary vector and enqueue its left and right children if they exist.Once all the nodes at a level are processed add this 1D temporary vector to the final 2D vector, representing that level. This process repeats until all levels are traversed. Finally, return this 2D vector containing the level order traversal of the binary tree.

Solution

Implementation

Live Editor

function Solution() {
function TreeNode(val = 0, left = null, right = null) {
    this.val = val;
    this.left = left;
    this.right = right;
}
function constructTreeFromArray(array) {
    if (!array.length) return null;
    
    let root = new TreeNode(array[0]);
    let queue = [root];
    let i = 1;

    while (i < array.length) {
        let currentNode = queue.shift();
        
        if (array[i] !== null) {
            currentNode.left = new TreeNode(array[i]);
            queue.push(currentNode.left);
        }
        i++;

        if (i < array.length && array[i] !== null) {
            currentNode.right = new TreeNode(array[i]);
            queue.push(currentNode.right);
        }
        i++;
    }
    return root;
}
function levelOrder(root) {
    if (!root) return [];
    
    const queue = [root];
    const ans = [];
    
    while (queue.length > 0) {
        const size = queue.length;
        const temp = [];
        
        for (let i = 0; i < size; i++) {
            const curr = queue.shift();
            
            if (curr.left) queue.push(curr.left);
            if (curr.right) queue.push(curr.right);
            
            temp.push(curr.val);
        }
        
        ans.push(temp);
    }
    
    return ans;
}


const array =  [3,9,20,null,null,15,7]
const input = constructTreeFromArray(array)
const output = levelOrder(input)
  return (
    <div>
      <p>
        <b>Input: </b>{JSON.stringify(array)}
      </p>
      <p>
        <b>Output:</b> {output.toString()}
      </p>
    </div>
  );
}

Result

Loading...

Code in Different Languages

JavaScript

Written by @hiteshgahanolia

}
function levelOrder(root) {
 if (!root) return [];
 
 const queue = [root];
 const ans = [];
 
 while (queue.length > 0) {
     const size = queue.length;
     const temp = [];
     
     for (let i = 0; i < size; i++) {
         const curr = queue.shift();
         
         if (curr.left) queue.push(curr.left);
         if (curr.right) queue.push(curr.right);
         
         temp.push(curr.val);
     }
     
     ans.push(temp);
 }
 
 return ans;
}

TypeScript

Written by @hiteshgahanolia

 class TreeNode {
  val: number;
  left: TreeNode | null;
  right: TreeNode | null;
  constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
      this.val = (val === undefined ? 0 : val);
      this.left = (left === undefined ? null : left);
      this.right = (right === undefined ? null : right);
  }
}

function levelOrder(root: TreeNode | null): number[][] {
  if (!root) return [];
  
  const queue: TreeNode[] = [root];
  const ans: number[][] = [];
  
  while (queue.length > 0) {
      const size = queue.length;
      const temp: number[] = [];
      
      for (let i = 0; i < size; i++) {
          const curr = queue.shift()!;
          
          if (curr.left) queue.push(curr.left);
          if (curr.right) queue.push(curr.right);
          
          temp.push(curr.val);
      }
      
      ans.push(temp);
  }
  
  return ans;
}

Python

Written by @hiteshgahanolia

from collections import deque
class TreeNode:
 def __init__(self, val=0, left=None, right=None):
     self.val = val
     self.left = left
     self.right = right

class Solution:
 def levelOrder(self, root: TreeNode) -> List[List[int]]:
     if not root:
         return []
     
     q = deque([root])
     ans = []
     
     while q:
         size = len(q)
         temp = []
         
         for _ in range(size):
             curr = q.popleft()
             
             if curr.left:
                 q.append(curr.left)
             if curr.right:
                 q.append(curr.right)
             
             temp.append(curr.val)
         
         ans.append(temp)
     
     return ans 

Java

Written by @hiteshgahanolia

import java.util.*;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> q = new LinkedList<>();
        List<List<Integer>> ans = new ArrayList<>();
        
        if (root == null) return ans;
        
        q.offer(root);
        
        while (!q.isEmpty()) {
            int size = q.size();
            List<Integer> temp = new ArrayList<>();
            
            for (int i = 0; i < size; i++) {
                TreeNode curr = q.poll();
                
                if (curr.left != null) q.offer(curr.left);
                if (curr.right != null) q.offer(curr.right);
                
                temp.add(curr.val);
            }
            
            ans.add(temp);
        }
        
        return ans;
    }
}

C++

Written by @hiteshgahanolia

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode *> q;
        vector<vector<int>> ans;
        
        if(!root) return ans;
        
        q.push(root);
        
        while(!q.empty()){
            int size = q.size();
            vector<int> temp;
            
            while(size--){
                TreeNode *curr = q.front();
                q.pop();
                
                if(curr->left) q.push(curr->left);
                if(curr->right) q.push(curr->right);
                
                temp.push_back(curr->val);
            }
            
            ans.push_back(temp);
        }
        
        return ans;
    }
};

Complexity Analysis

Time Complexity:

• $O(N)$ where N is the number of nodes in the binary tree. Each node of the binary tree is enqueued and dequeued exactly once, hence all nodes need to be processed and visited. Processing each node takes constant time operations which contributes to the overall linear time complexity.

Space Complexity:

• $O(N)$ where N is the number of nodes in the binary tree. In the worst case, the queue has to hold all the nodes of the last level of the binary tree, the last level could at most hold N/2 nodes hence the space complexity of the queue is proportional to $O(N)$.The resultant vector answer also stores the values of the nodes level by level and hence contains all the nodes of the tree contributing to O(N) space as well.

References

• LeetCode Problem: Binary Tree Level Order Traversal

• Solution Link: LeetCode Solution