Skip to main content

Recall: The Sensitivity Metric

Recall, also known as Sensitivity or True Positive Rate (TPR), measures the model's ability to find all the positive samples in a dataset. It answers the question: "Of all the actual positive cases that exist, how many did the model correctly identify?"

1. The Mathematical Formula​

Recall is calculated by dividing the number of correctly predicted positive results by the total number of actual positives (those we caught + those we missed).

Recall=TPTP+FN\text{Recall} = \frac{TP}{TP + FN}

Where:

  • TP (True Positives): Correctly predicted positive samples.
  • FN (False Negatives): The "Misses"—cases that were actually positive, but the model incorrectly labeled them as negative.

2. When Recall is the Top Priority​

You should prioritize Recall when the cost of a False Negative is extremely high. In these scenarios, it is better to have a few "false alarms" than to miss a single positive case.

Real-World Example: Cancer Detection​

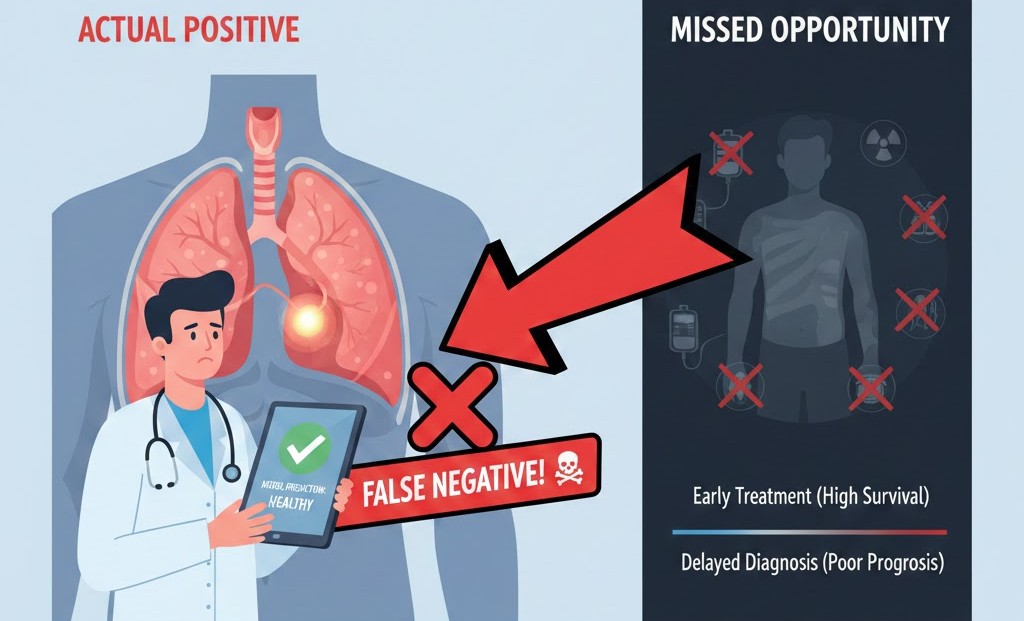
Cancer Detection
  • Positive Class: Patient has cancer.
  • False Negative: The patient has cancer, but the model says they are "Healthy."
  • The Consequence: The patient does not receive treatment, which could be fatal.
  • The Goal: We want 100% Recall. We would rather tell a healthy person they need more tests (False Positive) than tell a sick person they are fine (False Negative).

3. The Precision-Recall Inverse Relationship​

As you saw in the Precision module, there is an inherent trade-off.

  • To increase Recall: You can make your model "less strict." If a bank flags every transaction as potentially fraudulent, it will have 100% Recall (it caught every thief), but its Precision will be terrible (it blocked every honest customer too).
  • To increase Precision: You make the model "more strict," which inevitably leads to missing some positive cases, thereby lowering Recall.

4. Implementation with Scikit-Learn​

from sklearn.metrics import recall_score

# Actual target values (1 = Sick, 0 = Healthy)
y_true = [1, 1, 1, 0, 1, 0, 1]

# Model predictions
y_pred = [1, 0, 1, 0, 1, 0, 0]

# Calculate Recall
score = recall_score(y_true, y_pred)

print(f"Recall Score: {score:.2f}")
# Output: Recall Score: 0.60
# (We found 3 out of 5 sick people; we missed 2)

5. Summary Table: Precision vs. Recall​

MetricFocusGoalFailure Mode
PrecisionQuality"Don't cry wolf."High Precision misses many real cases.
RecallQuantity"Leave no one behind."High Recall creates many false alarms.

6. How to Balance Both?​

If you need a single number that accounts for both the "False Alarms" of Precision and the "Misses" of Recall, you need the F1-Score.

References​

Is your model struggling to choose between Precision and Recall? Let's look at the "middle ground" metric.