Jump Search (Geeks for Geeks)
What is Jump Search?
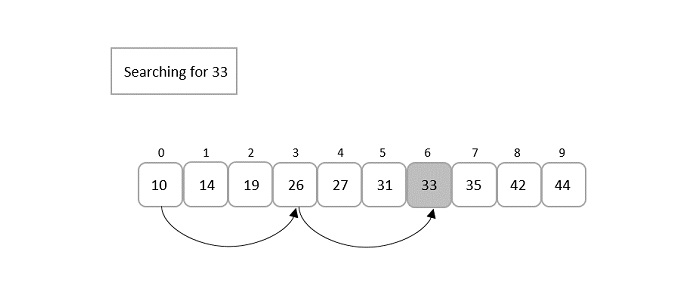
Jump Search is an efficient search algorithm for sorted arrays. It works by jumping ahead by fixed steps and then performing a linear search within a block, making it faster than linear search but less complex than binary search.
Algorithm for Jump Search
- Calculate the optimal step size , where is the length of the list.
- Start from the first element and jump ahead by the step size until the target element is greater than or equal to the current element.
- Perform a linear search within the identified block.
- If the target element is found, return its index.
- If the target element is not found, return -1.
How does Jump Search work?
- It calculates a jump step based on the length of the list.
- It jumps ahead in blocks, comparing the target value with the current element at each step.
- Once the block where the target might be located is identified, a linear search within the block is performed.
Problem Description
Given a sorted list and a target element, implement the Jump Search algorithm to find the index of the target element in the list. If the element is not present, return -1.
Examples
Example 1: Input: list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] target = 6 Output: 6
Example 2: Input: list = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] target = 15 Output: -1
Your Task:
You don't need to read input or print anything. Complete the function jump_search() which takes arr[], N and K as input parameters and returns the index of K in the array. If K is not present in the array, return -1.
Expected Time Complexity: Expected Auxiliary Space:
Constraints
Implementation
- Python
- C++
- Java
- JavaScript
import math
def jump_search(lst, target):
length = len(lst)
step = int(math.sqrt(length))
prev = 0
while lst[min(step, length) - 1] < target:
prev = step
step += int(math.sqrt(length))
if prev >= length:
return -1
for i in range(prev, min(step, length)):
if lst[i] == target:
return i
return -1
#include <iostream>
#include <cmath>
#include <vector>
int jump_search(const std::vector<int>& lst, int target) {
int length = lst.size();
int step = sqrt(length);
int prev = 0;
while (lst[std::min(step, length) - 1] < target) {
prev = step;
step += sqrt(length);
if (prev >= length) {
return -1;
}
}
for (int i = prev; i < std::min(step, length); ++i) {
if (lst[i] == target) {
return i;
}
}
return -1;
}
int main() {
std::vector<int> lst = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
int target = 6;
std::cout << "Index: " << jump_search(lst, target) << std::endl;
return 0;
}
import java.util.Arrays;
public class JumpSearch {
public static int jumpSearch(int[] lst, int target) {
int length = lst.length;
int step = (int) Math.sqrt(length);
int prev = 0;
while (lst[Math.min(step, length) - 1] < target) {
prev = step;
step += (int) Math.sqrt(length);
if (prev >= length) {
return -1;
}
}
for (int i = prev; i < Math.min(step, length); i++) {
if (lst[i] == target) {
return i;
}
}
return -1;
}
public static void main(String[] args) {
int[] lst = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
int target = 6;
System.out.println("Index: " + jumpSearch(lst, target));
}
}
function jumpSearch(lst, target) {
let length = lst.length;
let step = Math.floor(Math.sqrt(length));
let prev = 0;
while (lst[Math.min(step, length) - 1] < target) {
prev = step;
step += Math.floor(Math.sqrt(length));
if (prev >= length) {
return -1;
}
}
for (let i = prev; i < Math.min(step, length); i++) {
if (lst[i] === target) {
return i;
}
}
return -1;
}
const lst = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
const target = 6;
console.log("Index:", jumpSearch(lst, target));
Complexity Analysis
- Time Complexity: , where is the number of elements in the list. The list is divided into blocks, leading to a root-time complexity.
- Space Complexity: , as no extra space is required apart from the input list.
Advantages and Disadvantages
Advantages:
- Faster than linear search for large sorted lists.
- Simpler than binary search while still being efficient.
Disadvantages:
- Requires the list to be sorted.
- Less efficient compared to binary search in terms of time complexity.