Diagonal Traverse

Problem Description

Given an m x n matrix mat, return an array of all the elements of the array in a diagonal order.

Examples

Example 1:

Input: mat = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,4,7,5,3,6,8,9]

Example 2:

Input: mat = [[1,2],[3,4]]
Output: [1,2,3,4]

Constraints

• m == mat.length
• n == mat[i].length
• $1 \leq m, n \leq 10^4$
• $1 \leq m * n \leq 10^4$
• $-10^5 \leq mat[i][j] \leq 10^5$

Solution for Diagonal Traverse

Approach 1: Diagonal Iteration and Reversal

Intuition

A common strategy for solving a lot of programming problem is to first solve a stripped down, simpler version of them and then think what needs to be changed to achieve the original goal. Our first approach to this problem is also based on this very idea. So, instead of thinking about the zig-zag pattern of printing for the diagonals, let's say the problem statement simply asked us to print out the contents of the matrix, one diagonal after the other starting from the first element. Let's see what this problem would look like.

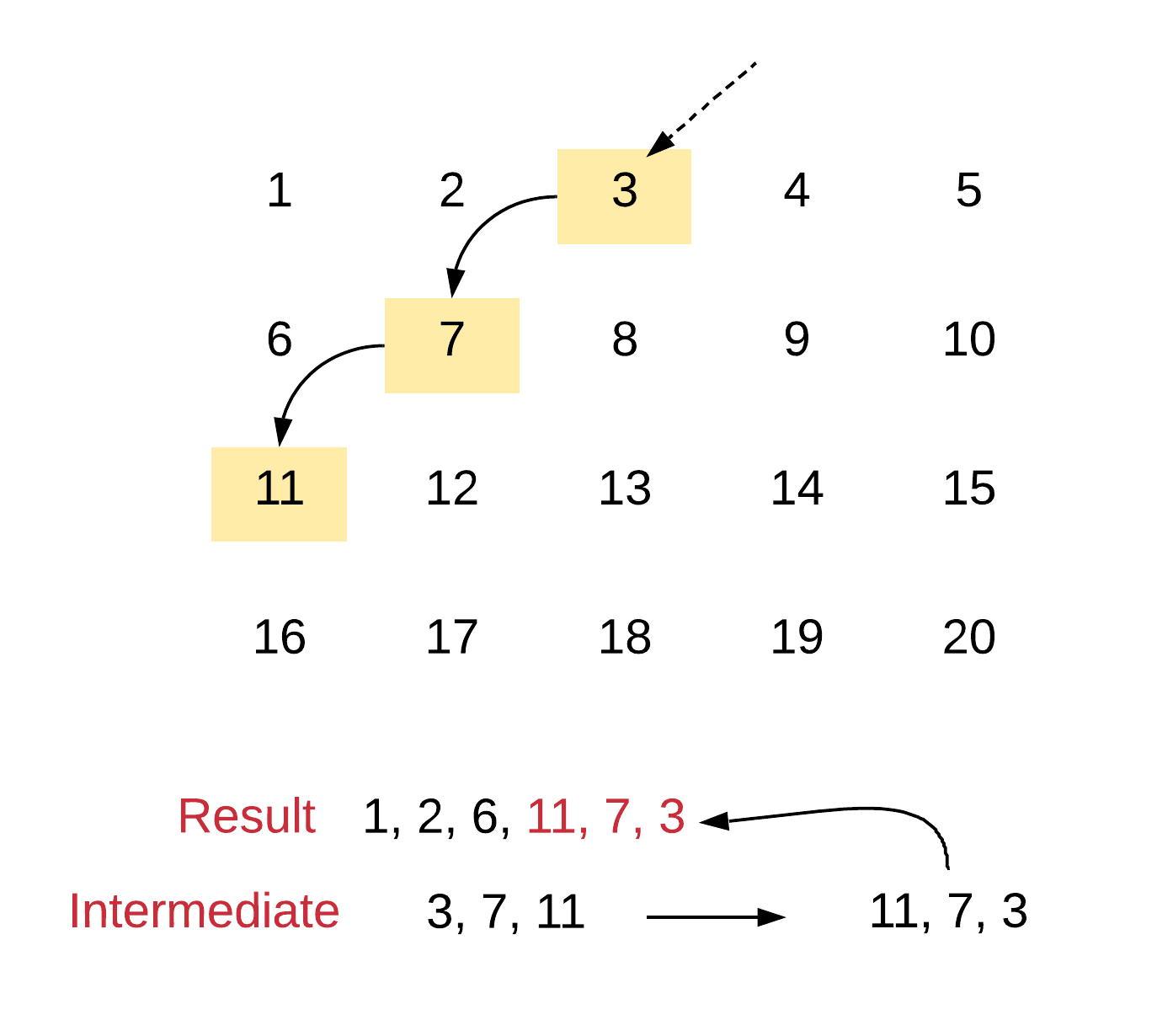
The first row and the last column in this problem would serve as the starting point for the corresponding diagonal. Given an element inside a diagonal, say [i,j], we can either go up the diagonal by going one row up and one column ahead i.e. [i−1,j+1] or, we can go down the diagonal by going one row down and one column to the left i.e. [i+1,j−1]. Note that this applies to diagonals that go from right to left only. The math would change for the ones that go from left to right.

This is a simple problem to solve, right? The only difference between this one and the original problem is that some of the diagonals are not printed in the right order. That's all we need to fix to get the right solution!

Algorithm

1. Initialize a result array that we will eventually return.

2. We would have an outer loop that will go over each of the diagonals one by one. As mentioned before, the elements in the first row and the last column would actually be the heads of their corresponding diagonals.

3. We then have an inner while loop that iterates over all the elements in the diagonal. We can calculate the number of elements in the corresponding diagonal by doing some math but we can simply iterate until one of the indices goes out of bounds.

4. For each diagonal we will need a new list or dynamic array like data structure since we don't know what size to allocate. Again, we can do some math and calculate the size of that particular diagonal and allocate memory; but it's not necessary for this explanation.

5. For odd numbered diagonals, we simply need to add the elements in our intermediary array, in reverse order to the final result array.

Code in Different Languages

C++

Written by @Shreyash3087

#include <vector>
#include <algorithm>

class Solution {
public:
    std::vector<int> findDiagonalOrder(std::vector<std::vector<int>>& matrix) {
        // Check for empty matrices
        if (matrix.empty() || matrix[0].empty()) {
            return std::vector<int>();
        }
        
        // Variables to track the size of the matrix
        int N = matrix.size();
        int M = matrix[0].size();
        
        // The vector to store the result
        std::vector<int> result(N * M);
        int k = 0;
        std::vector<int> intermediate;
        
        // We have to go over all the elements in the first
        // row and the last column to cover all possible diagonals
        for (int d = 0; d < N + M - 1; ++d) {
            // Clear the intermediate vector every time we start
            // to process another diagonal
            intermediate.clear();
            
            // We need to figure out the "head" of this diagonal
            // The elements in the first row and the last column
            // are the respective heads.
            int r = d < M ? 0 : d - M + 1;
            int c = d < M ? d : M - 1;
            
            // Iterate until one of the indices goes out of scope
            // Take note of the index math to go down the diagonal
            while (r < N && c > -1) {
                intermediate.push_back(matrix[r][c]);
                ++r;
                --c;
            }
                
            // Reverse even numbered diagonals. The
            // article says we have to reverse odd 
            // numbered articles but here, the numbering
            // is starting from 0 :P
            if (d % 2 == 0) {
                std::reverse(intermediate.begin(), intermediate.end());
            }
            
            // Copy elements from the intermediate vector to the result array
            for (int i = 0; i < intermediate.size(); ++i) {
                result[k++] = intermediate[i];
            }
        }
        return result;
    }
};

Java

Written by @Shreyash3087

class Solution {
    public int[] findDiagonalOrder(int[][] matrix) {
        
        // Check for empty matrices
        if (matrix == null || matrix.length == 0) {
            return new int[0];
        }
        
        // Variables to track the size of the matrix
        int N = matrix.length;
        int M = matrix[0].length;
        
        // The two arrays as explained in the algorithm
        int[] result = new int[N*M];
        int k = 0;
        ArrayList<Integer> intermediate = new ArrayList<Integer>();
        
        // We have to go over all the elements in the first
        // row and the last column to cover all possible diagonals
        for (int d = 0; d < N + M - 1; d++) {
            
            // Clear the intermediate array every time we start
            // to process another diagonal
            intermediate.clear();
            
            // We need to figure out the "head" of this diagonal
            // The elements in the first row and the last column
            // are the respective heads.
            int r = d < M ? 0 : d - M + 1;
            int c = d < M ? d : M - 1;
            
            // Iterate until one of the indices goes out of scope
            // Take note of the index math to go down the diagonal
            while (r < N && c > -1) {
                
                intermediate.add(matrix[r][c]);
                ++r;
                --c;
            }
                
            // Reverse even numbered diagonals. The
            // article says we have to reverse odd 
            // numbered articles but here, the numbering
            // is starting from 0 :P
            if (d % 2 == 0) {
                Collections.reverse(intermediate);
            }
            
            for (int i = 0; i < intermediate.size(); i++) {
                result[k++] = intermediate.get(i);
            }
        }
        return result;
    }
}

Python

Written by @Shreyash3087

class Solution:
    
    def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:
        
        # Check for empty matrices
        if not matrix or not matrix[0]:
            return []
        
        # Variables to track the size of the matrix
        N, M = len(matrix), len(matrix[0])
        
        # The two arrays as explained in the algorithm
        result, intermediate = [], []
        
        # We have to go over all the elements in the first
        # row and the last column to cover all possible diagonals
        for d in range(N + M - 1):
            
            # Clear the intermediate array everytime we start
            # to process another diagonal
            intermediate.clear()
            
            # We need to figure out the "head" of this diagonal
            # The elements in the first row and the last column
            # are the respective heads.
            r, c = 0 if d < M else d - M + 1, d if d < M else M - 1
            
            # Iterate until one of the indices goes out of scope
            # Take note of the index math to go down the diagonal
            while r < N and c > -1:
                intermediate.append(matrix[r][c])
                r += 1
                c -= 1
            
            # Reverse even numbered diagonals. The
            # article says we have to reverse odd 
            # numbered articles but here, the numbering
            # is starting from 0 :P
            if d % 2 == 0:
                result.extend(intermediate[::-1])
            else:
                result.extend(intermediate)
        return result        

Complexity Analysis

Time Complexity: $O(N.M)$

Reason: considering an array with N rows and M columns, where odd numbered diagonals are processed twice due to element reversal, requiring O(K) for array clearing, making the overall complexity remain O(N⋅M).

Space Complexity: $O(min(N,M))$

Reason: as extra space is utilized by intermediate arrays storing diagonal elements, with a maximum space of min(N,M), as diagonals extend till one index goes out of scope.

Approach 2: Simulation

Intuition

This approach simply and plainly does what the problem statement asks us to do. It's pure simulation. However, in order to implement this simulation, we need to understand the walking patterns inside the array. Basically, in the previous approach, figuring out the head of the diagonal was pretty easy. In this case, it won't be that easy. We need to figure out two things for each diagonal:

1. The direction in which we want to process it's elements and
2. The head or the starting point for the diagonal depending upon its direction.

Let's see these two things annotated on a sample matrix.

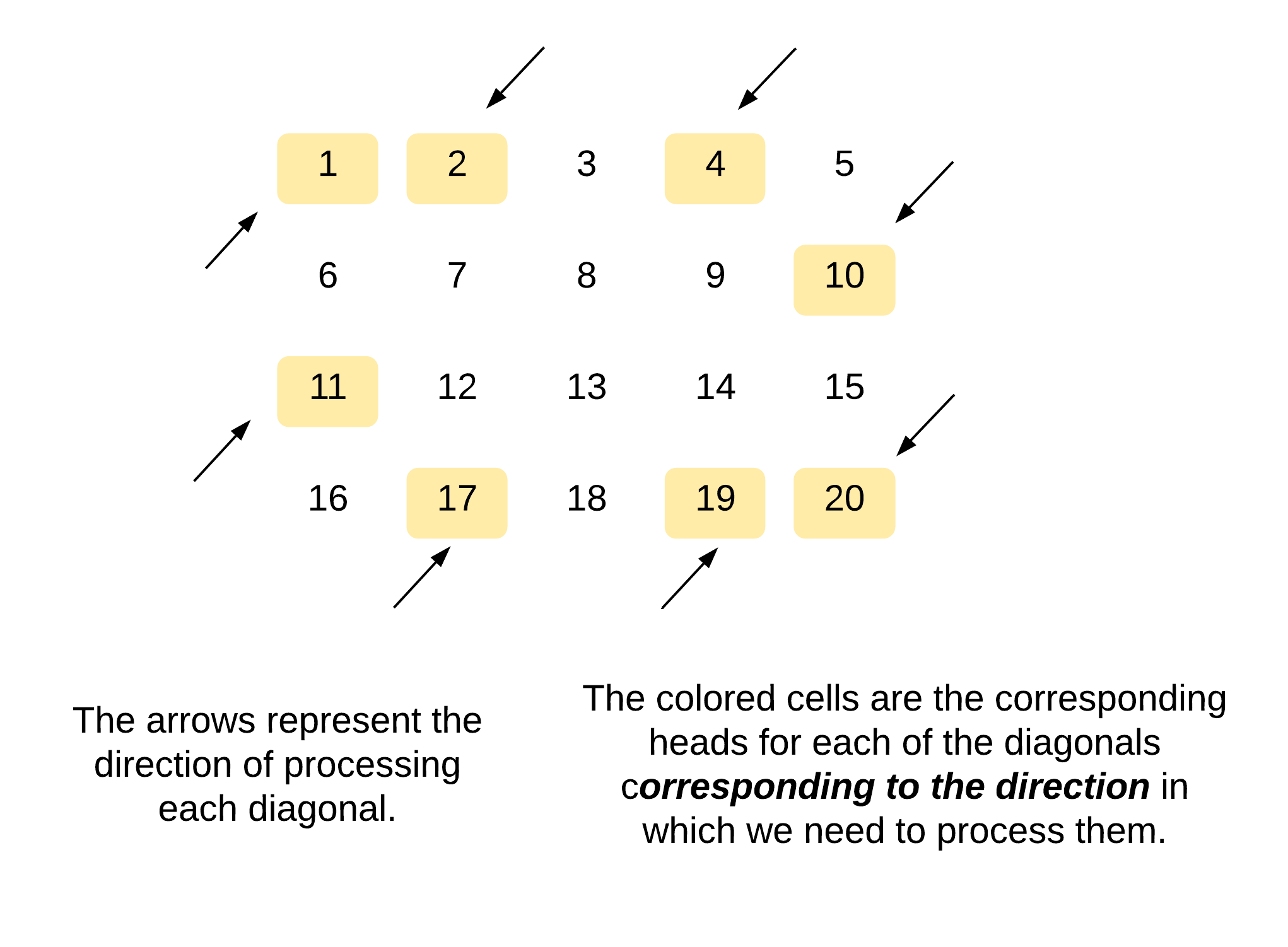
Now that we know what two things we need to figure out, let's get to the part where we actually do it! The direction is pretty straightforward. We can simply use a boolean variable and keep alternating it to figure out the direction for a diagonal. That part is sorted. The slightly tricky part is figuring out the head of the next diagonal.

The good part is, we already know the end of the previous diagonal. We can use that information to figure out the head of the next diagonal.

Next head when going UP Let's look at the two scenarios that we may come across when we are at the tail end of a downwards diagonal and we want to find the head of the next diagonal.

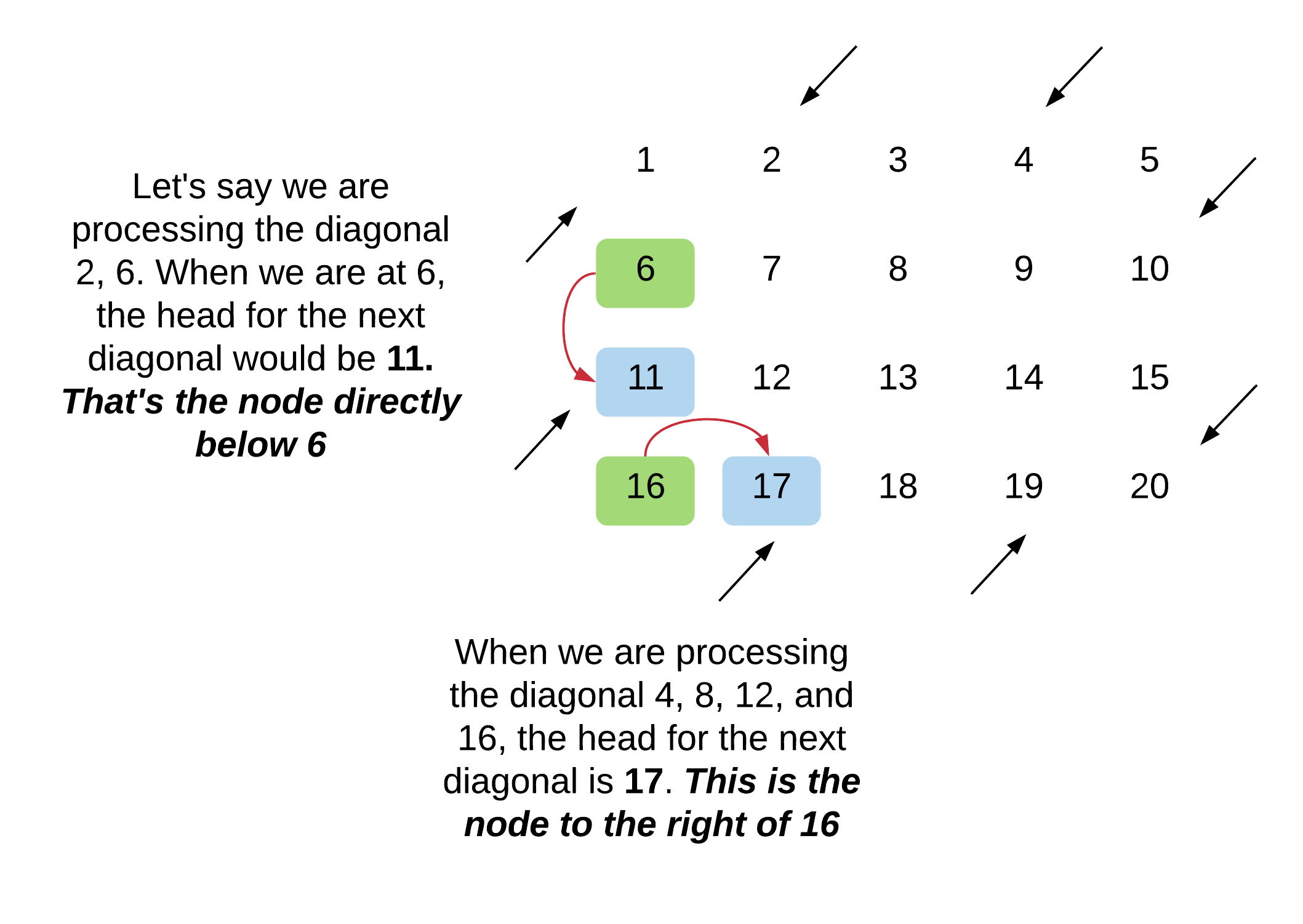
So, the general rule that we will be following when we want to find the head for an upwards going diagonal is that:

The head would be the node directly below the tail of the previous diagonal. Unless the tail lies in the last row of the matrix in which case the head would be the node right next to the tail.

Next head when going DOWN Let's look at the two scenarios that we may come across when we are at the tail end of an upwards diagonal and we want to find the head of the next diagonal.

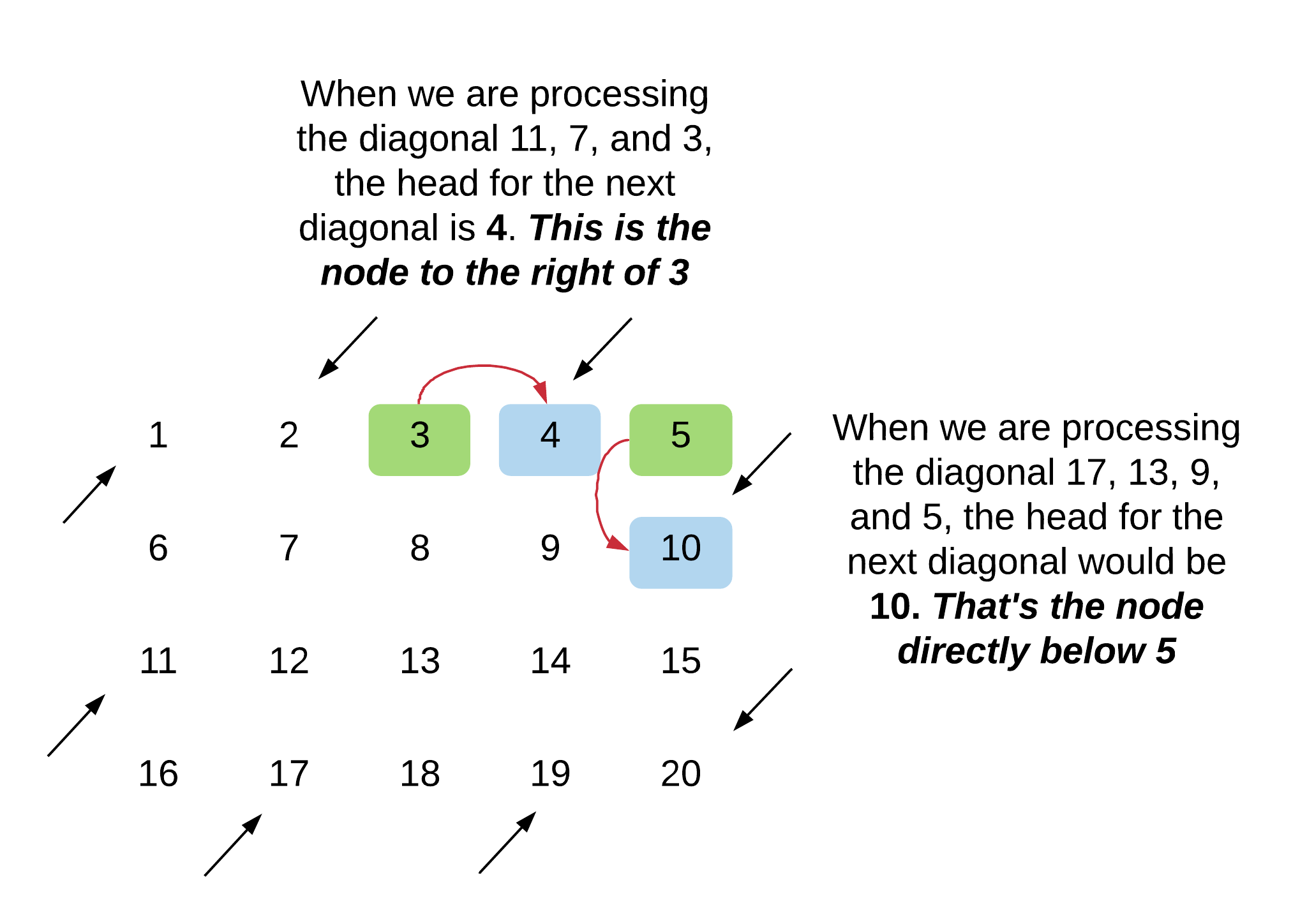
So, the general rule that we will be following when we want to find the head for a downwards going diagonal is that:

The head would be the node to the right of the tail of the previous diagonal. Unless the tail lies in the last column of the matrix in which case the head would be the node directly below the tail.

Code in Different Languages

C++

Written by @Shreyash3087

#include <vector>

class Solution {
public:
    std::vector<int> findDiagonalOrder(std::vector<std::vector<int>>& matrix) {
        // Check for empty matrices
        if (matrix.empty() || matrix[0].empty()) {
            return std::vector<int>();
        }

        // Variables to track the size of the matrix
        int N = matrix.size();
        int M = matrix[0].size();

        // Indices that will help us progress through
        // the matrix, one element at a time.
        int row = 0, column = 0;

        // As explained in the article, this is the variable
        // that helps us keep track of what direction we are
        // processing the current diagonal
        int direction = 1;

        // The final result array
        std::vector<int> result(N * M);
        int r = 0;

        // The uber while loop which will help us iterate over all
        // the elements in the array.
        while (row < N && column < M) {

            // First and foremost, add the current element to
            // the result matrix.
            result[r++] = matrix[row][column];

            // Move along in the current diagonal depending upon
            // the current direction.[i, j] -> [i - 1, j + 1] if
            // going up and [i, j] -> [i + 1][j - 1] if going down.
            int new_row = row + (direction == 1 ? -1 : 1);
            int new_column = column + (direction == 1 ? 1 : -1);

            // Checking if the next element in the diagonal is within the
            // bounds of the matrix or not. If it's not within the bounds,
            // we have to find the next head.
            if (new_row < 0 || new_row == N || new_column < 0 || new_column == M) {

                // If the current diagonal was going in the upwards
                // direction.
                if (direction == 1) {

                    // For an upwards going diagonal having [i, j] as its tail
                    // If [i, j + 1] is within bounds, then it becomes
                    // the next head. Otherwise, the element directly below
                    // i.e. the element [i + 1, j] becomes the next head
                    row += (column == M - 1 ? 1 : 0);
                    column += (column < M - 1 ? 1 : 0);

                } else {

                    // For a downwards going diagonal having [i, j] as its tail
                    // if [i + 1, j] is within bounds, then it becomes
                    // the next head. Otherwise, the element directly below
                    // i.e. the element [i, j + 1] becomes the next head
                    column += (row == N - 1 ? 1 : 0);
                    row += (row < N - 1 ? 1 : 0);
                }

                // Flip the direction
                direction = 1 - direction;

            } else {

                row = new_row;
                column = new_column;
            }
        }
        return result;
    }
};

Java

Written by @Shreyash3087

class Solution {
    public int[] findDiagonalOrder(int[][] matrix) {
        
        // Check for empty matrices
        if (matrix == null || matrix.length == 0) {
            return new int[0];
        }
        
        // Variables to track the size of the matrix
        int N = matrix.length;
        int M = matrix[0].length;
        
        // Incides that will help us progress through 
        // the matrix, one element at a time.
        int row = 0, column = 0;
        
        // As explained in the article, this is the variable
        // that helps us keep track of what direction we are
        // processing the current diaonal
        int direction = 1;
        
         // The final result array
        int[] result = new int[N*M];
        int r = 0;
        
        // The uber while loop which will help us iterate over all
        // the elements in the array.
        while (row < N && column < M) {
            
            // First and foremost, add the current element to 
            // the result matrix. 
            result[r++] = matrix[row][column];
            
            // Move along in the current diagonal depending upon
            // the current direction.[i, j] -> [i - 1, j + 1] if 
            // going up and [i, j] -> [i + 1][j - 1] if going down.
            int new_row = row + (direction == 1 ? -1 : 1);
            int new_column = column + (direction == 1 ? 1 : -1);
            
            // Checking if the next element in the diagonal is within the
            // bounds of the matrix or not. If it's not within the bounds,
            // we have to find the next head. 
            if (new_row < 0 || new_row == N || new_column < 0 || new_column == M) {
                
                // If the current diagonal was going in the upwards
                // direction.
                if (direction == 1) {
                    
                    // For an upwards going diagonal having [i, j] as its tail
                    // If [i, j + 1] is within bounds, then it becomes
                    // the next head. Otherwise, the element directly below
                    // i.e. the element [i + 1, j] becomes the next head
                    row += (column == M - 1 ? 1 : 0) ;
                    column += (column < M - 1 ? 1 : 0);
                        
                } else {
                    
                    // For a downwards going diagonal having [i, j] as its tail
                    // if [i + 1, j] is within bounds, then it becomes
                    // the next head. Otherwise, the element directly below
                    // i.e. the element [i, j + 1] becomes the next head
                    column += (row == N - 1 ? 1 : 0);
                    row += (row < N - 1 ? 1 : 0);
                }
                    
                // Flip the direction
                direction = 1 - direction;        
                        
            } else {
                
                row = new_row;
                column = new_column;
            }
        }
        return result;      
    }
}

Python

Written by @Shreyash3087

class Solution:
    
    def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:
        
        # Check for an empty matrix
        if not matrix or not matrix[0]:
            return []
        
        # The dimensions of the matrix
        N, M = len(matrix), len(matrix[0])
        
        # Incides that will help us progress through 
        # the matrix, one element at a time.
        row, column = 0, 0
        
        # As explained in the article, this is the variable
        # that helps us keep track of what direction we are
        # processing the current diaonal
        direction = 1
        
        # Final result array that will contain all the elements
        # of the matrix
        result = []
        
        # The uber while loop which will help us iterate over all
        # the elements in the array.
        while row < N and column < M:
            
            # First and foremost, add the current element to 
            # the result matrix. 
            result.append(matrix[row][column])
            
            # Move along in the current diagonal depending upon
            # the current direction.[i, j] -> [i - 1, j + 1] if 
            # going up and [i, j] -> [i + 1][j - 1] if going down.
            new_row = row + (-1 if direction == 1 else 1)
            new_column = column + (1 if direction == 1 else -1)
            
            # Checking if the next element in the diagonal is within the
            # bounds of the matrix or not. If it's not within the bounds,
            # we have to find the next head. 
            if new_row < 0 or new_row == N or new_column < 0 or new_column == M:
                
                # If the current diagonal was going in the upwards
                # direction.
                if direction:
                    
                    # For an upwards going diagonal having [i, j] as its tail
                    # If [i, j + 1] is within bounds, then it becomes
                    # the next head. Otherwise, the element directly below
                    # i.e. the element [i + 1, j] becomes the next head
                    row += (column == M - 1)
                    column += (column < M - 1)
                else:
                    
                    # For a downwards going diagonal having [i, j] as its tail
                    # if [i + 1, j] is within bounds, then it becomes
                    # the next head. Otherwise, the element directly below
                    # i.e. the element [i, j + 1] becomes the next head
                    column += (row == N - 1)
                    row += (row < N - 1)
                    
                # Flip the direction
                direction = 1 - direction        
            else:
                row = new_row
                column = new_column
                        
        return result                      

Complexity Analysis

Time Complexity: $O(N.M)$

Reason: since we process each element of the matrix exactly once.

Space Complexity: $O(1)$

Reason: since we don't make use of any additional data structure.

References

• LeetCode Problem: Diagonal Traverse

• Solution Link: Diagonal Traverse

---

Authors:

Loading...