Skip to main content

Path with Maximum Probability

Problem Description​

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

Examples​

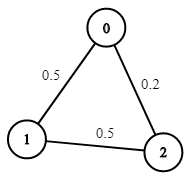
Example 1: image

Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

Example 2: image

Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000

Constraints​

  • 2 <= n <= 10^4
  • 0 <= start, end < n
  • start != end
  • 0 <= a, b < n
  • a != b
  • 0 <= succProb.length == edges.length <= 2*10^4
  • 0 <= succProb[i] <= 1
  • There is at most one edge between every two nodes.

Solution for Path with Maximum Probability Problem​

Approach​

Main Intuition​

The main intuition behind this code is similar to Dijkstra's algorithm for finding the shortest path, but instead of minimizing distances, it maximizes probabilities. The idea is to iteratively explore the most probable paths using a priority queue to always expand the most promising node (the node with the highest probability of being part of the maximum probability path to the end node).

Graph Representation:​

  • The graph is represented using an adjacency list. Each node has a list of pairs, where each pair consists of an adjacent node and the probability of successfully traversing the edge to that node.

Input Parsing:​

  • The number of nodes (n) and the edges along with their respective probabilities (edges and succProb) are given as input.
  • The start and end nodes are also provided.

Building the Graph:​

  • A vector of vectors of pairs (adj) is created to store the adjacency list.
  • For each edge, two entries are added to the adjacency list to ensure the graph is undirected. Each entry contains the adjacent node and the probability of traversing that edge.

Probability Initialization:​

  • A prob vector is initialized to store the maximum probability of reaching each node from the start node. It is initialized to 0.0 for all nodes.
  • The probability of reaching the start node from itself is set to 1.0 (prob[start] = 1.0).

Priority Queue for Processing Nodes:​

  • A priority queue (pq) is used to process nodes. This queue helps in processing nodes in the order of their probabilities (although the current implementation uses a max-heap for integer priorities, which is not correct and should use a min-heap for probabilities).

Dijkstra-like Algorithm:​

  • The algorithm processes nodes from the priority queue. For each node, it checks all its adjacent nodes.
  • For each adjacent node, it calculates the probability of reaching it through the current node (prob[node] * probab).
  • If this new probability is higher than the currently known probability for the adjacent node, it updates the probability and pushes the adjacent node into the priority queue.

Result:​

  • After processing all reachable nodes, the maximum probability to reach the end node is found in prob[end].

Implementation​

Live Editor
function Solution(arr) {
var maxProbability = function(n, edges, succProb, start, end) {
    const p = Array(n).fill(0);
    const graph = p.reduce((m, _, i) => m.set(i, []), new Map());
    edges.forEach(([u, v], i) => {
        graph.get(u).push([v, succProb[i]]);
        graph.get(v).push([u, succProb[i]]);
    });
    
    const queue = [[start, 1]];
    p[start] = 1;
    
    for (let [node, currP] of queue) {   
        for (let [adj, nextP] of graph.get(node)) {
        if (currP * nextP > p[adj]) {
            p[adj] = currP * nextP;
            queue.push([adj, p[adj]]);
        }
        }
    }
    
    return p[end];
};
  const input = [[0,1],[1,2],[0,2]]
  const n = 3
  const succProb = [0.5,0.5,0.2]
  const start=0;
  const end =2
  const output = maxProbability(n, input , succProb,start , end)
  return (
    <div>
      <p>
        <b>Input: </b>
        {JSON.stringify(input)}
      </p>
      <p>
        <b>Output:</b> {output.toString()}
      </p>
    </div>
  );
}
Result
Loading...

Complexity Analysis​

  • Time Complexity: O(edges∗log(n))O(edges*log(n))
  • Space Complexity: O(n) O(n)

Code in Different Languages​

Written by @hiteshgahanolia
function maxProbability(n, edges, succProb, start, end) {
 let adj = Array.from({ length: n }, () => []);

 for (let i = 0; i < edges.length; i++) {
     adj[edges[i][0]].push([edges[i][1], succProb[i]]);
     adj[edges[i][1]].push([edges[i][0], succProb[i]]);
 }

 let prob = new Array(n).fill(0.0);
 let pq = new MaxPriorityQueue({ priority: x => x[1] });

 prob[start] = 1.0;
 pq.enqueue([start, 1.0]);

 while (!pq.isEmpty()) {
     let [node, nodeProb] = pq.dequeue().element;

     for (let [adjNode, probab] of adj[node]) {
         if (prob[node] * probab > prob[adjNode]) {
             prob[adjNode] = prob[node] * probab;
             pq.enqueue([adjNode, prob[adjNode]]);
         }
     }
 }

 return prob[end];
}

References​