Open the Lock

Problem Description

You have a lock in front of you with 4 circular wheels. Each wheel has 10 slots: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'. The wheels can rotate freely and wrap around: for example we can turn '9' to be '0', or '0' to be '9'. Each move consists of turning one wheel one slot.

The lock initially starts at '0000', a string representing the state of the 4 wheels.

You are given a list of deadends dead ends, meaning if the lock displays any of these codes, the wheels of the lock will stop turning and you will be unable to open it.

Given a target representing the value of the wheels that will unlock the lock, return the minimum total number of turns required to open the lock, or -1 if it is impossible.

Examples

Example 1:

Input: deadends = ["0201","0101","0102","1212","2002"], target = "0202"
Output: 6
Explanation: 
A sequence of valid moves would be "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202".
Note that a sequence like "0000" -> "0001" -> "0002" -> "0102" -> "0202" would be invalid,
because the wheels of the lock become stuck after the display becomes the dead end "0102".

Example 2:

Input: deadends = ["8888"], target = "0009"
Output: 1
Explanation: We can turn the last wheel in reverse to move from "0000" -> "0009".

Constraints

• 1 <= deadends.length <= 500
• deadends[i].length == 4
• target.length == 4
• target will not be in the list deadends.
• target and deadends[i] consist of digits only.

Solution for Open the Lock

Overview

For simplicity, let's say any combination of any state of all wheels represents one lock combination. e.g. '0000', '1000', '2000', ... etc. all represent a lock combination.

Say we are currently at combination '0000', and we make one wheel turn. Now we are at combination 1000. This combination change due to one wheel turn can be visualized as traversing a graph from node 1 (combination '0000') to node 2 (combination '1000').

It can be better understood with the help of the following image:

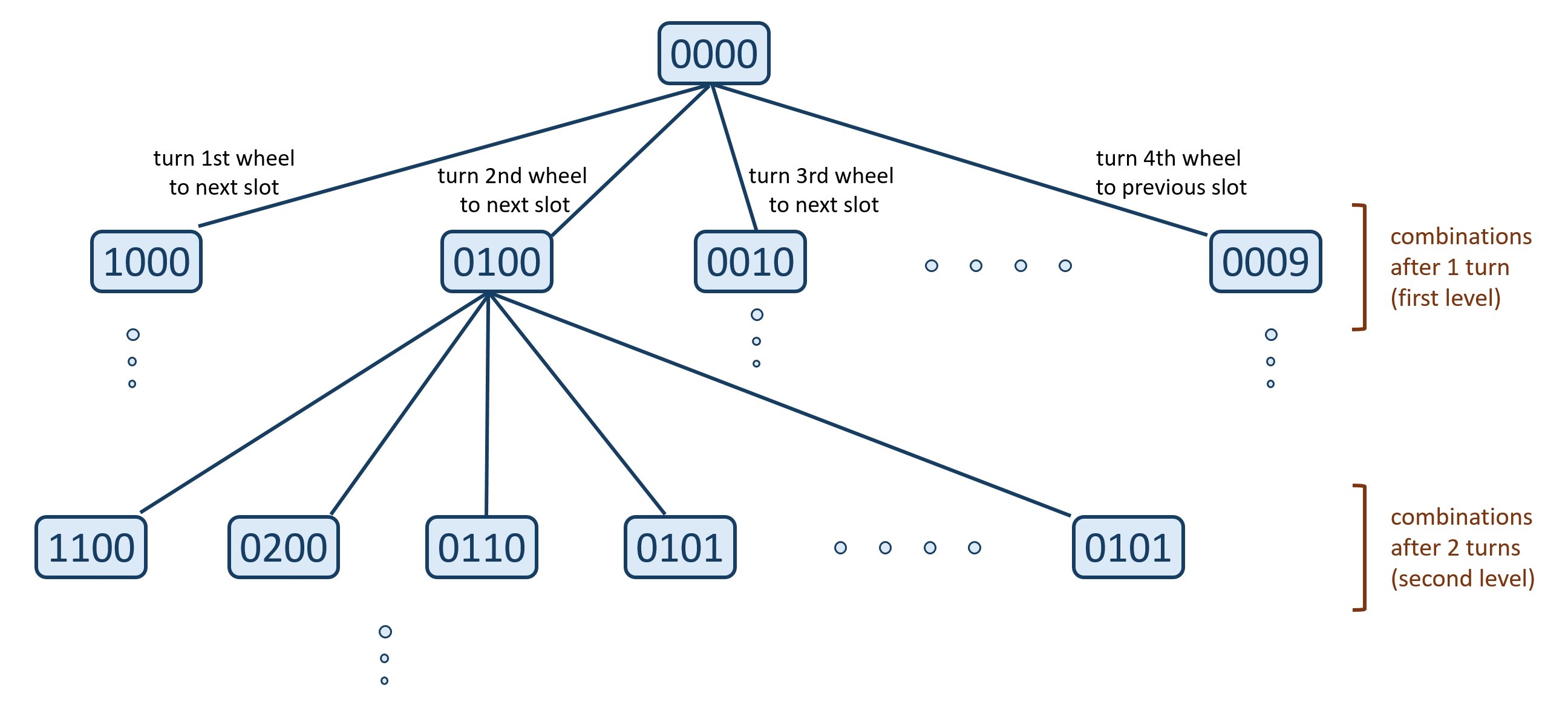
In this graph, each node represents a lock combination, and the edge represents one wheel turn.

According to the problem statement, we start from the lock combination '0000'. We can make one wheel turn at a time and need to find the minimum steps required to reach the target lock combination.

As we observed, each lock combination is a graph's node, and each wheel turn is an edge connecting two nodes. The given problem statement can be re-worded as: "We start from node lock combination '0000' and have to find the minimum number of edges to traverse to reach the target lock combination node." Thus, the given problem can be converted into a graph traversal problem.

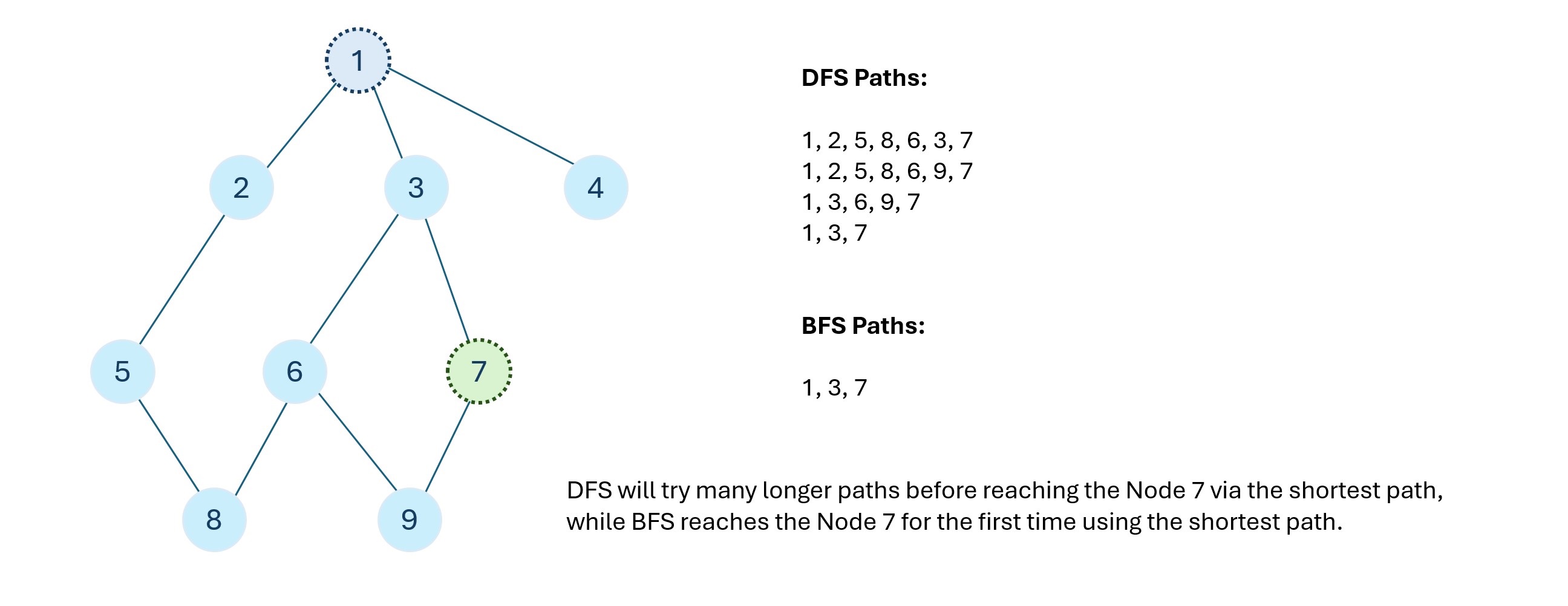
To traverse nodes in a graph, we mainly utilize two algorithms: depth-first search (DFS), and breadth-first search (BFS). If you are new to these algorithms we recommend reading our Depth-First Search and Breadth-First Search explore cards.

We can solve this problem using both traversals, but given the constraints, the depth-first search will result in a TLE. This is because DFS explores as deeply as possible along each branch before backtracking. It doesn't necessarily explore nodes in any particular order; it might go deep into a branch before exploring other branches.

BFS is well-suited for finding the shortest path in unweighted graphs, which makes it a good fit for this problem because BFS explores nodes level by level. It starts from the source node and explores all its neighbors before moving on to the next level of neighbors. Due to its level-order exploration strategy, BFS guarantees that the first time it reaches a node, it has found the shortest path to that node.

Approach: Breadth-First Search

Intuition

We will keep a queue, pending_combinations, containing the lock combinations yet to be visited using BFS. Initially, it will contain the starting combination '0000'.

We will visit each combination stored in the queue one by one. If the current popped combination is the target combination, we will return the number of edges traversed (number of wheel turns we made) to reach this combination. BFS guarantees the shortest path in an unweighted graph, so as soon as we find an answer, we know it is the optimal one. Otherwise, we will generate new combinations from the current combination, by rotating each of the four wheels to the next slot digit and the previous slot digit one by one. Then we will push the new combinations into the queue.

We will keep two additional data structures to quickly fetch the next and the previous slot digits for the current slot digits whenever needed.

Notice that we might reach the same lock combinations, again and again, using different paths, and these duplicate combinations will always generate the same next combinations.

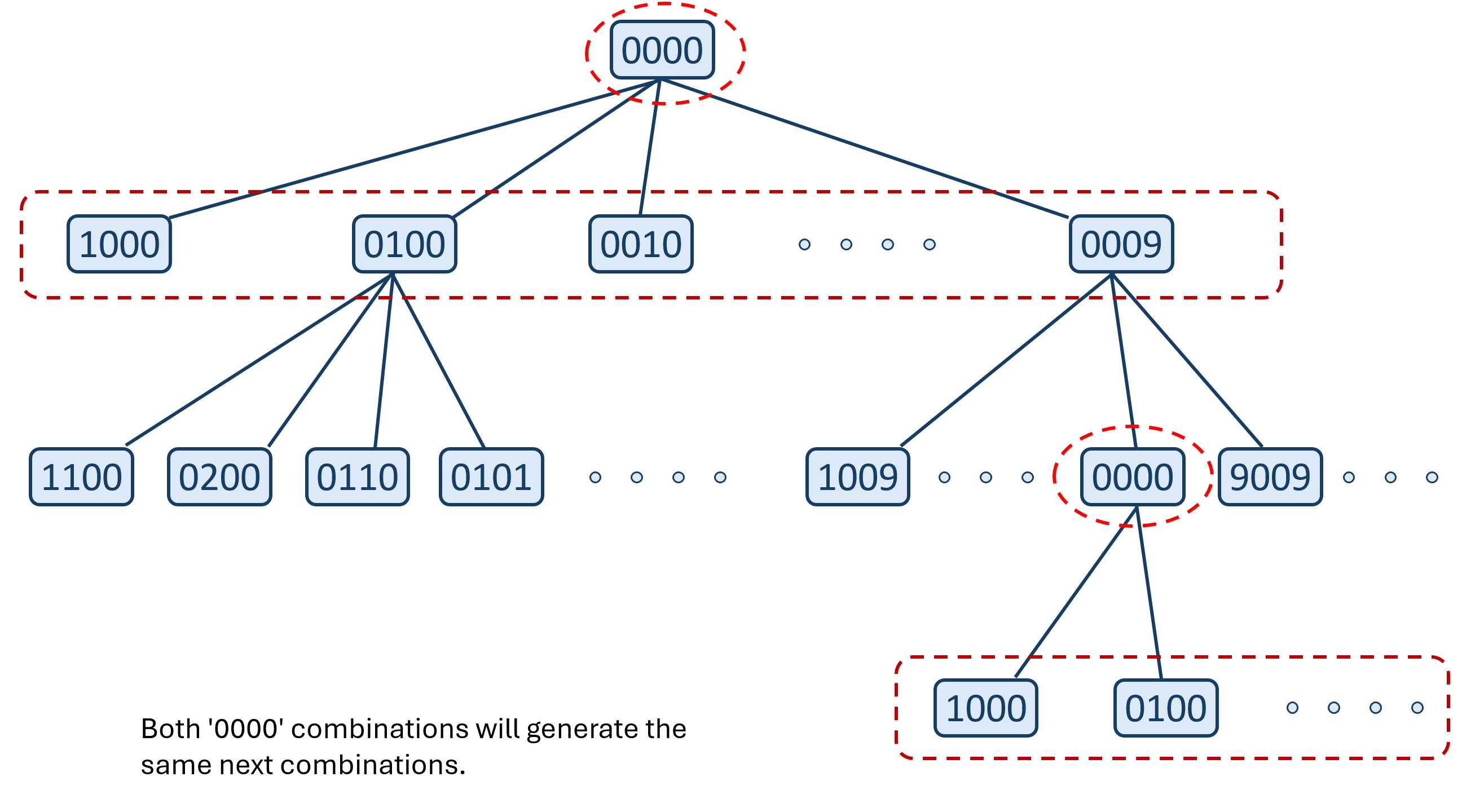
So, we will keep one additional data structure to mark visited combinations to avoid traversing on a combination more than once. We also have some dead-end combinations from which we can't proceed further. We can consider these combinations as visited combinations because we cannot generate new combinations using these combinations.

Thus, we will keep a hash set visited_combinations, insert the dead-end combinations in it initially, and will insert the visited combinations while doing the BFS.

Algorithm

1. Initialization:

   • Create two character maps, next_slot to map the current slot digit with its next slot digit, and prev_slot to map the current slot digit with its previous slot digit.
   • Create a hash set visited_combinations, initially containing all deadends array combinations.
   • Create a queue pending_combinations to traverse all combinations in level-wise BFS.
   • Create an integer variable turns initially storing 0, to denote the number of wheel turns made.

2. If visited_combinations contains the starting combination '0000' then we can never reach the target combination and will return -1.

3. Insert the starting combination '0000' in the queue and mark it as visited.

4. While there are elements in the queue, iterate on all current level combinations using a for loop:

   • Pop the current combination from the front of the queue.
   • If the current combination is the target combination return turns.
   • Otherwise, iterate on all four wheels; for each wheel, generate the new combination by turning the respective wheel to the next slot and the previous slot. If the new combination is not present in visited_combinations then push it in the queue and mark it as visited.
   • After iterating on all current level combinations increment turns by 1.

5. If we never reach the target combination, then, return -1.

Code in Different Languages

C++

Written by @Shreyash3087

class Solution {
public:
    int openLock(vector<string>& deadends, string target) {
        // Map the next slot digit for each current slot digit.
        unordered_map<char, char> nextSlot = {
            {'0', '1'}, 
            {'1', '2'}, 
            {'2', '3'}, 
            {'3', '4'}, 
            {'4', '5'},
            {'5', '6'}, 
            {'6', '7'}, 
            {'7', '8'}, 
            {'8', '9'}, 
            {'9', '0'}
        };
        // Map the previous slot digit for each current slot digit.
        unordered_map<char, char> prevSlot = {
            {'0', '9'}, 
            {'1', '0'}, 
            {'2', '1'}, 
            {'3', '2'}, 
            {'4', '3'},
            {'5', '4'}, 
            {'6', '5'}, 
            {'7', '6'}, 
            {'8', '7'}, 
            {'9', '8'}
        };

        // Hash set to store visited and dead-end combinations.
        unordered_set<string> visitedCombinations(deadends.begin(), deadends.end());
        // Queue to store combinations generated after each turn.
        queue<string> pendingCombinations;

        // Count the number of wheel turns made.
        int turns = 0;

        // If the starting combination is also a dead-end, 
        // then we can't move from the starting combination.
        if (visitedCombinations.find("0000") != visitedCombinations.end()) {
            return -1;
        }

        // Start with the initial combination '0000'.
        pendingCombinations.push("0000");
        visitedCombinations.insert("0000");

        while (!pendingCombinations.empty()) {
            // Explore all the combinations of the current level.
            for (int currLevelNodesCount = pendingCombinations.size();
                 currLevelNodesCount > 0; --currLevelNodesCount) {
                // Get the current combination from the front of the queue.
                string currentCombination = pendingCombinations.front();
                pendingCombinations.pop();

                // If the current combination matches the target, 
                // return the number of turns/level.
                if (currentCombination == target) {
                    return turns;
                }

                // Explore all possible new combinations by turning each wheel in both directions.
                for (int wheel = 0; wheel < 4; wheel += 1) {
                    // Generate the new combination by turning the wheel to the next digit.
                    string newCombination = currentCombination;
                    newCombination[wheel] = nextSlot[newCombination[wheel]];
                    // If the new combination is not a dead-end and was never visited, 
                    // add it to the queue and mark it as visited.
                    if (visitedCombinations.find(newCombination) == visitedCombinations.end()) {
                        pendingCombinations.push(newCombination);
                        visitedCombinations.insert(newCombination);
                    }

                    // Generate the new combination by turning the wheel to the previous digit.
                    newCombination = currentCombination;
                    newCombination[wheel] = prevSlot[newCombination[wheel]];
                    // If the new combination is not a dead-end and is never visited, 
                    // add it to the queue and mark it as visited.
                    if (visitedCombinations.find(newCombination) == visitedCombinations.end()) {
                        pendingCombinations.push(newCombination);
                        visitedCombinations.insert(newCombination);
                    }
                }
            }
            // We will visit the next-level combinations.
            turns += 1;
        }
        // We never reached the target combination.
        return -1;
    }
};

Java

Written by @Shreyash3087

class Solution {
    public int openLock(String[] deadends, String target) {
        // Map the next slot digit for each current slot digit.
        Map<Character, Character> nextSlot = Map.of(
            '0', '1', 
            '1', '2', 
            '2', '3', 
            '3', '4', 
            '4', '5', 
            '5', '6', 
            '6', '7', 
            '7', '8', 
            '8', '9', 
            '9', '0'
        );
        // Map the previous slot digit for each current slot digit.
        Map<Character, Character> prevSlot = Map.of(
            '0', '9', 
            '1', '0', 
            '2', '1', 
            '3', '2', 
            '4', '3', 
            '5', '4', 
            '6', '5', 
            '7', '6', 
            '8', '7', 
            '9', '8'
        );

        // Set to store visited and dead-end combinations.
        Set<String> visitedCombinations = new HashSet<>(Arrays.asList(deadends));
        // Queue to store combinations generated after each turn.
        Queue<String> pendingCombinations = new LinkedList<String>();

        // Count the number of wheel turns made.
        int turns = 0;

        // If the starting combination is also a dead-end, 
        // then we can't move from the starting combination.
        if (visitedCombinations.contains("0000")) {
            return -1;
        }

        // Start with the initial combination '0000'.
        pendingCombinations.add("0000");
        visitedCombinations.add("0000");

        while (!pendingCombinations.isEmpty()) {
            // Explore all the combinations of the current level.
            int currLevelNodesCount = pendingCombinations.size();
            for (int i = 0; i < currLevelNodesCount; i++) {
                // Get the current combination from the front of the queue.
                String currentCombination = pendingCombinations.poll();

                // If the current combination matches the target, 
                // return the number of turns/level.
                if (currentCombination.equals(target)) {
                    return turns;
                }

                // Explore all possible new combinations by turning each wheel in both directions.
                for (int wheel = 0; wheel < 4; wheel += 1) {
                    // Generate the new combination by turning the wheel to the next digit.
                    StringBuilder newCombination = new StringBuilder(currentCombination);
                    newCombination.setCharAt(wheel, nextSlot.get(newCombination.charAt(wheel)));
                    // If the new combination is not a dead-end and was never visited, 
                    // add it to the queue and mark it as visited.
                    if (!visitedCombinations.contains(newCombination.toString())) {
                        pendingCombinations.add(newCombination.toString());
                        visitedCombinations.add(newCombination.toString());
                    }

                    // Generate the new combination by turning the wheel to the previous digit.
                    newCombination = new StringBuilder(currentCombination);
                    newCombination.setCharAt(wheel, prevSlot.get(newCombination.charAt(wheel)));
                    // If the new combination is not a dead-end and is never visited, 
                    // add it to the queue and mark it as visited.
                    if (!visitedCombinations.contains(newCombination.toString())) {
                        pendingCombinations.add(newCombination.toString());
                        visitedCombinations.add(newCombination.toString());
                    }
                }
            }
            // We will visit next-level combinations.
            turns += 1;
        }
        // We never reached the target combination.
        return -1;
    }
}

Python

Written by @Shreyash3087

class Solution:
    def openLock(self, deadends: List[str], target: str) -> int:
        # Map the next slot digit for each current slot digit.
        next_slot = {
            "0": "1",
            "1": "2",
            "2": "3",
            "3": "4",
            "4": "5",
            "5": "6",
            "6": "7",
            "7": "8",
            "8": "9",
            "9": "0",
        }
        # Map the previous slot digit for each current slot digit.
        prev_slot = {
            "0": "9",
            "1": "0",
            "2": "1",
            "3": "2",
            "4": "3",
            "5": "4",
            "6": "5",
            "7": "6",
            "8": "7",
            "9": "8",
        }

        # Set to store visited and dead-end combinations.
        visited_combinations = set(deadends)
        # Queue to store combinations generated after each turn.
        pending_combinations = deque()

        # Count the number of wheel turns made.
        turns = 0

        # If the starting combination is also a dead-end, 
        # then we can't move from the starting combination.
        if "0000" in visited_combinations:
            return -1

        # Start with the initial combination '0000'.
        pending_combinations.append("0000")
        visited_combinations.add("0000")

        while pending_combinations:
            # Explore all combinations of the current level.
            curr_level_nodes_count = len(pending_combinations)
            for _ in range(curr_level_nodes_count):
                # Get the current combination from the front of the queue.
                current_combination = pending_combinations.popleft()

                # If the current combination matches the target, 
                # return the number of turns/level.
                if current_combination == target:
                    return turns

                # Explore all possible new combinations 
                # by turning each wheel in both directions.
                for wheel in range(4):
                    # Generate the new combination 
                    # by turning the wheel to the next digit.
                    new_combination = list(current_combination)
                    new_combination[wheel] = next_slot[new_combination[wheel]]
                    new_combination_str = "".join(new_combination)
                    # If the new combination is not a dead-end and 
                    # was never visited, 
                    # add it to the queue and mark it as visited.
                    if new_combination_str not in visited_combinations:
                        pending_combinations.append(new_combination_str)
                        visited_combinations.add(new_combination_str)

                    # Generate the new combination 
                    # by turning the wheel to the previous digit.
                    new_combination = list(current_combination)
                    new_combination[wheel] = prev_slot[new_combination[wheel]]
                    new_combination_str = "".join(new_combination)
                    # If the new combination is not a dead-end and 
                    # is never visited, 
                    # add it to the queue and mark it as visited.
                    if new_combination_str not in visited_combinations:
                        pending_combinations.append(new_combination_str)
                        visited_combinations.add(new_combination_str)

            # We will visit next-level combinations.
            turns += 1

        # We never reached the target combination.
        return -1

Complexity Analysis

Time Complexity: $O(4(d+10^4))$

Reason:

• Initializing the hash maps with n key-value pairs, and the hash set with d combinations of length w will take $O(2 \cdot n)$ and $O(d \cdot w)$ time respectively.
• In the worst case, we might iterate on all $n^w$ unique combinations, and for each combination, we perform $2 \cdot w$. Thus, it will take $O(n^w \cdot 2 \cdot w)=O(n^w \cdot w)$ time.
• So, this approach will take $O(n+(d+n^w) \cdot w) = O(10+(d+10^4) \cdot 4) = O(4(d+10^4))$ time.

Space Complexity: $O(4(d+10^4))$

Reason:

• The hash maps with n key-value pairs, and the hash set with d combinations of length w will take $O(2 \cdot n)$ and $O(d \cdot w)$ space respectively.
• In the worst case, we might push all $n^w$ wunique combinations of length w in the queue and the hash set. Thus, it will take $O(n^w \cdot w)$ space.
• So, this approach will take $O(n+(d+n^w) \cdot w) = O(4(d+10^4))$ space.

Video Solution

References

• LeetCode Problem: Open the Lock

• Solution Link: Open the Lock

---

Authors:

Loading...