Skip to main content

Coin Change

Problem Description​

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money. Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1. You may assume that you have an infinite number of each kind of coin.

Examples​

Example 1:

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

Example 3:

Input: coins = [1], amount = 0
Output: 0

Constraints​

  • 1 <= coins.length <= 12
  • 1 <= coins[i] <= 231 - 1
  • 0 <= amount <= 104

Solution for Coin Change Problem​

Brute Force - Recursion​

Intuition​

Now, take a look at what the coin change problem is all about.

You are given a sequence of coins of various denominations as part of the coin change problem. For example, consider the following array a collection of coins, with each element representing a different denomination.

Example​

{ 2, 3, 5, 10, 20, 30, 50 }

Our goal is to use these coins to accumulate a certain amount of money while using the fewest (or optimal) coins. Furthermore, you can assume that a given denomination has an infinite number of coins. To put it another way, you can use a specific denomination as many times as you want.

For example, if you want to reach 78 using the above denominations, you will need the four coins listed below.

{ 3, 5, 20, 50 }

Solution Using Recursion​

You have two options for each coin: include it or exclude it.

coins[] = {1, 2, 3} sum = 4

When you include a coin, you add its value to the current sum solution(sol+coins[i], I, and if it is not equal, you move to the next coin, i.e., the next recursive call solution(sol, i++).

Total solutions are 2.

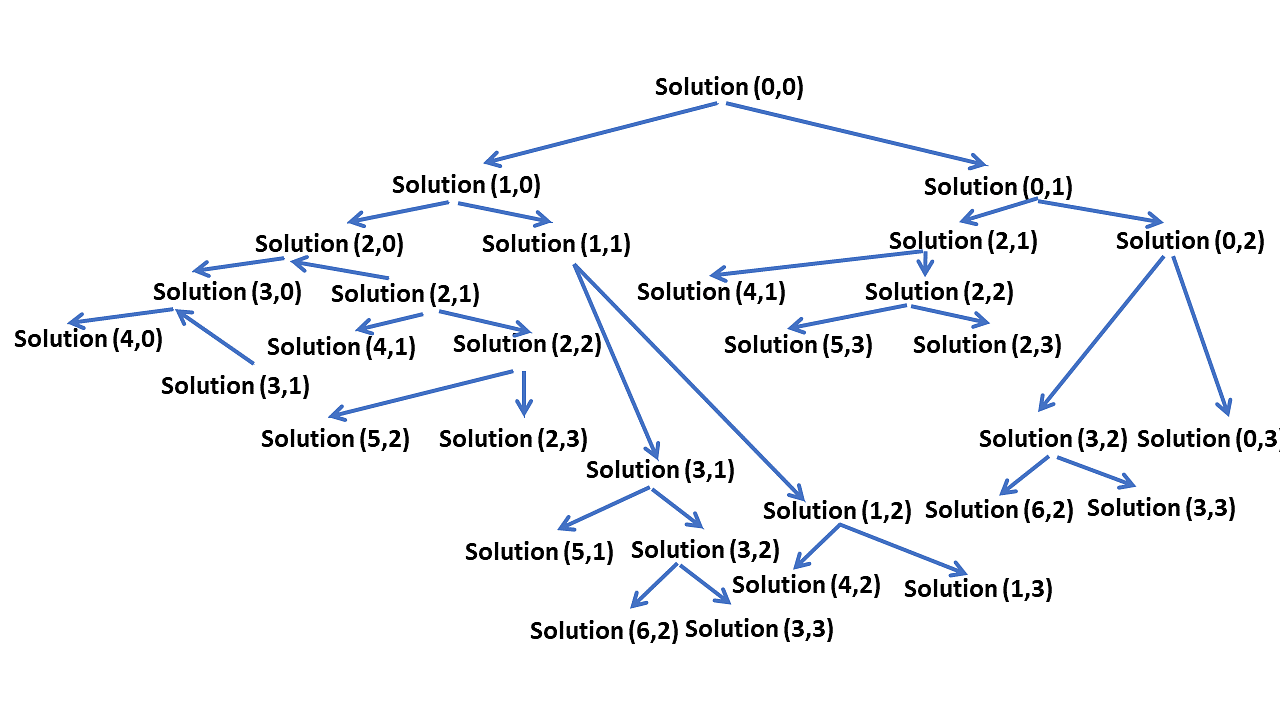
The diagram below depicts the recursive calls made during program execution. image

Implementation​

Live Editor
function coinChangeWrapper(arr) {
  function solve(coins, index, sum) {
        if (sum === 0) return 0;

        if (index < 0 || sum < 0) return Number.MAX_SAFE_INTEGER;

        // Not take the current coin
        let notTake = solve(coins, index - 1, sum);
        
        // Take the current coin
        let take = Number.MAX_SAFE_INTEGER;
        if (sum >= coins[index]) {
            let result = solve(coins, index, sum - coins[index]);
            if (result !== Number.MAX_SAFE_INTEGER) {
                take = 1 + result;
            }
        }

        return Math.min(take, notTake);
    }

    function coinChange(coins, amount) {
        let ans = solve(coins, coins.length - 1, amount);
        if (ans === Number.MAX_SAFE_INTEGER) return -1;
        return ans;
    }


  const input = [1,2,3]
  const sum = 4
  const output = coinChange(input ,sum)
  return (
    <div>
      <p>
        <b>Input: </b>{ JSON.stringify(input)}
      </p>
      <p>
        <b>Output:</b> {output.toString()}
      </p>
    </div>
  );
}
Result
Loading...

Code in Different Languages​

Written by @hiteshgahanolia
function solve(coins, index, sum) {
     if (sum === 0) return 0;

     if (index < 0 || sum < 0) return Number.MAX_SAFE_INTEGER;

     // Not take the current coin
     let notTake = solve(coins, index - 1, sum);
     
     // Take the current coin
     let take = Number.MAX_SAFE_INTEGER;
     if (sum >= coins[index]) {
         let result = solve(coins, index, sum - coins[index]);
         if (result !== Number.MAX_SAFE_INTEGER) {
             take = 1 + result;
         }
     }

     return Math.min(take, notTake);
 }

 function coinChange(coins, amount) {
     let ans = solve(coins, coins.length - 1, amount);
     if (ans === Number.MAX_SAFE_INTEGER) return -1;
     return ans;
 }

Complexity Analysis​

  • Time Complexity: O(2n)O(2^n) is the time complexity, where n is the number of coins , because it has Overlapping subproblems
  • Space Complexity: This approach doesn't need any auxilary space, but it maintains a recusion stack internally. If we consider the recursion tree, there is a repetition of a few sub-trees.

Optimized Approach - Memoization​

Intuition​

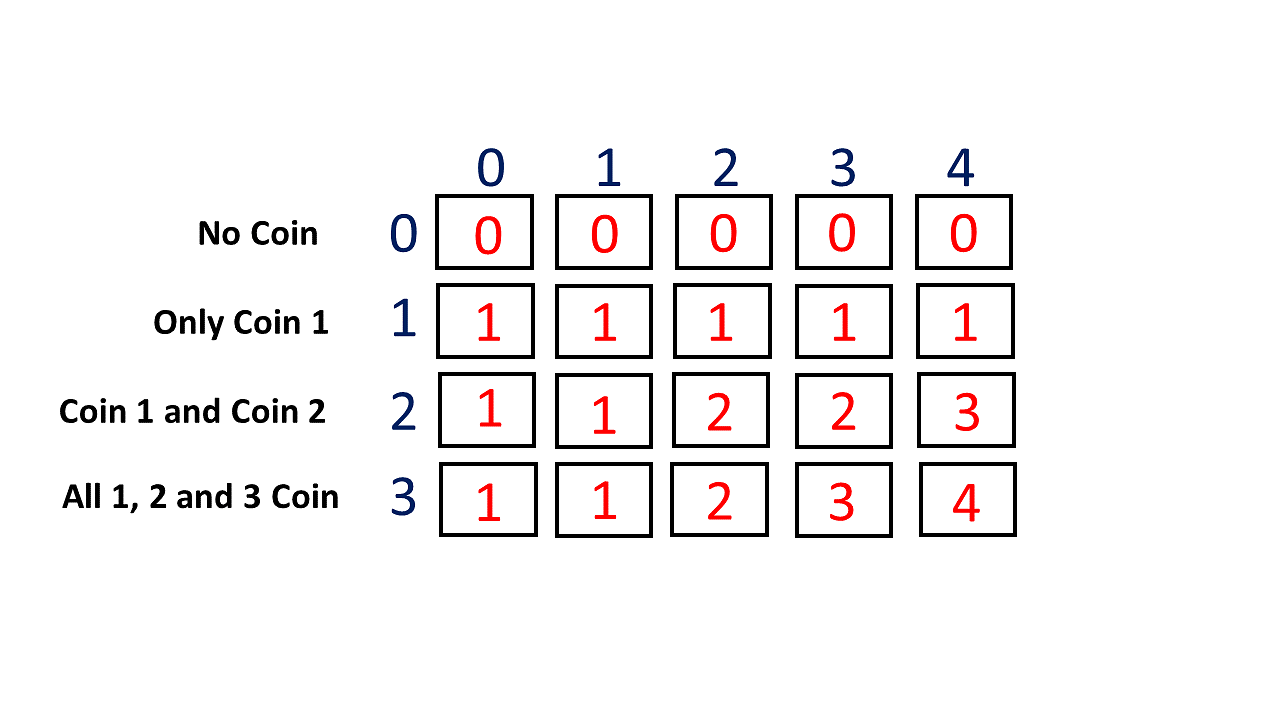
Can we recursive calls which are repeating ? The dynamic approach to solving the coin change problem is similar to the dynamic method used to solve the 0/1 Knapsack problem. To store the solution to the subproblem, you must use a 2D array (i.e. table). Then, take a look at the image below. image

Written by @hiteshgahanolia
int solve(vector<int>& coins, int index, int amount, vector<vector<int>>& dp) {
 if (amount == 0) return 0;
 if (amount < 0 || index < 0) return INT_MAX;

 if (dp[index][amount] != -1) return dp[index][amount];

 // Take the current coin
 int take = INT_MAX;
 if (amount >= coins[index]) {
     int result = solve(coins, index, amount - coins[index], dp);
     if (result != INT_MAX) {
         take = 1 + result;
     }
 }

 // Not take the current coin
 int notTake = solve(coins, index - 1, amount, dp);

 // Memoize the result
 dp[index][amount] = min(take, notTake);

 return dp[index][amount];
}

int coinChange(vector<int>& coins, int amount) {
 int n = coins.size();
 vector<vector<int>> dp(n, vector<int>(amount + 1, -1));
 int ans = solve(coins, n - 1, amount, dp);
 return ans == INT_MAX ? -1 : ans;
}

Complexity Analysis​

  • Time Complexity: O(N∗A) O(N*A)
    • Reason: There are NA states therefore at max ‘NA’ new problems will be solved. A is amount.
  • Space Complexity: O(N∗A)+O(N) O(N*A) + O(N)
    • Reason: We are using a recursion stack space(O(N)) and a 2D array ( O(N*A)).

Using Tabulation Method​

Intuition​

  • In the tabulation approach, we'll create a table (or array) to store solutions for all possible subproblems.
  • We'll fill up this table iteratively, starting from the smallest subproblems and gradually moving towards the main problem.
  • At each step, we'll use the solutions of already solved subproblems to find solutions for larger subproblems.
  • Finally, the solution to the main problem will be found at the last entry of the table.

Iterative Process​

  • We'll iterate through each amount of money starting from 0 up to the target amount.
  • For each amount, we'll iterate through each coin denomination and calculate the minimum number of coins required to make that amount using the current coin denomination.
  • We'll fill up the table progressively until we reach the target amount.
Written by @hiteshgahanolia
int coinChange(vector<int>& coins, int amount) {
     int dp[coins.size() + 1][amount + 1];
     for (int i = 0; i < coins.size() + 1; i++) {
         for (int j = 0; j < amount + 1; j++) {

             if (i == 0) {
                 dp[i][j] = INT_MAX - 1;
             }
             if (j == 0) {
                 dp[i][j] = 0;
             }
         }
     }
     for (int i = 1; i < coins.size() + 1; i++) {
         for (int j = 1; j < amount + 1; j++) {
             if (coins[i - 1] <= j) {
                 dp[i][j] = min(dp[i][j - coins[i - 1]] + 1, dp[i - 1][j]);
             } else {
                 dp[i][j] = dp[i - 1][j];
             }
         }
     }

     if (dp[coins.size()][amount] == INT_MAX - 1) {
         return -1;
     }

     return dp[coins.size()][amount];
 }
  • Here Time and Space Complexity are same as memoized approach.

References​